During the autumn of 1944, the US Air Corps forecasting team made a series of perfect predictions about weather patterns over the Pacific Ocean. Or so it seemed according to reports from aircrafts flying between Siberia and Guam. One of the forecasters, a mathematician called Edward Lorenz, soon complained about the apparent success rate: it was clear that the busy pilots were simply repeating the forecast as the observation.
Much of Lorenz’s frustration came from his belief that good predictions required good information. Without accurate reports, they could not understand the weather system, and without understanding the system, it was impossible to make reliable forecasts.
Monday afternoon’s tornado in Oklahoma City has shown how difficult it can be to predict weather in advance. Residents had just 16 minutes warning before the tornado hit. But why is it so hard to forecast extreme weather?
The nature of chaos
After World War Two, Lorenz took a position at the Massachusetts Institute of Technology, where he continued his work on weather dynamics. During those years, he derived a simple set of equations to describe airflow in the atmosphere. In 1961, he used a computer to simulate this airflow and made a curious discovery.
Lorenz found that if he ran two simulations with almost – but not quite – identical starting conditions, the results would always diverge eventually. In other words, if he wanted to reproduce an earlier set of results, he would need to know the exact initial state of the atmosphere in the previous simulation.
The diagram below shows two different trajectories of an air particle simulated from Lorenz’s equations. The black dots show the starting positions; the red and blue dots show where they end up after a set period of time.
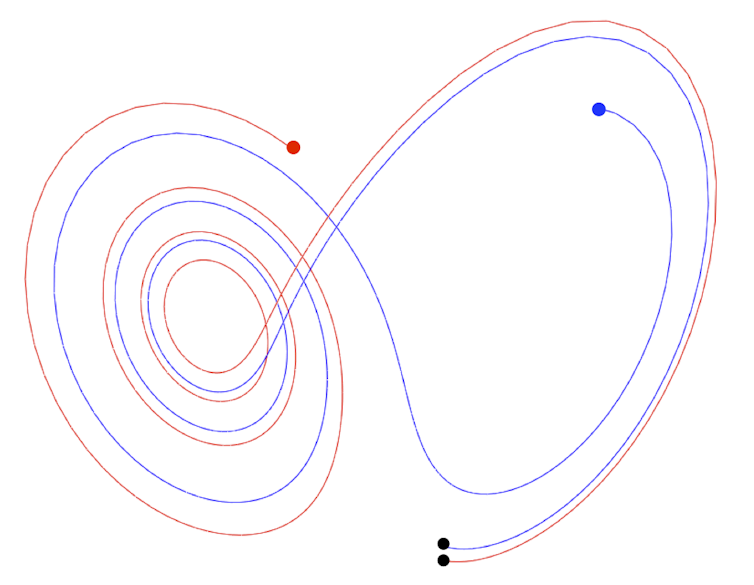
Lorenz noted that if the atmosphere really suffered from this “sensitive dependence on initial conditions”, accurate long-term weather predictions would be impossible. Even with vast amounts of information, reality would inevitably drift away from the forecast.
Sensitive dependence on initial conditions is more commonly known as the “butterfly effect”. A term coined after Lorenz gave a talk titled: “Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?”.
Of course, this is not to say that a butterfly will cause a tornado. Merely that two otherwise identical weather systems – one in which the butterfly flaps its wings, and one in which it does not – will eventually end up looking very different.
Lorenz’s work helped lay the foundations for the field of chaos theory. But there is more to chaos theory than the butterfly effect. For something to meet the mathematical definition of “chaotic”, it does not just need to be sensitive to initial conditions. It also needs to have an underlying structure.
For example, if we simulate Lorenz’s equations over a long period of time, each particle – regardless of where it starts – will eventually trace out the same “attractor”:
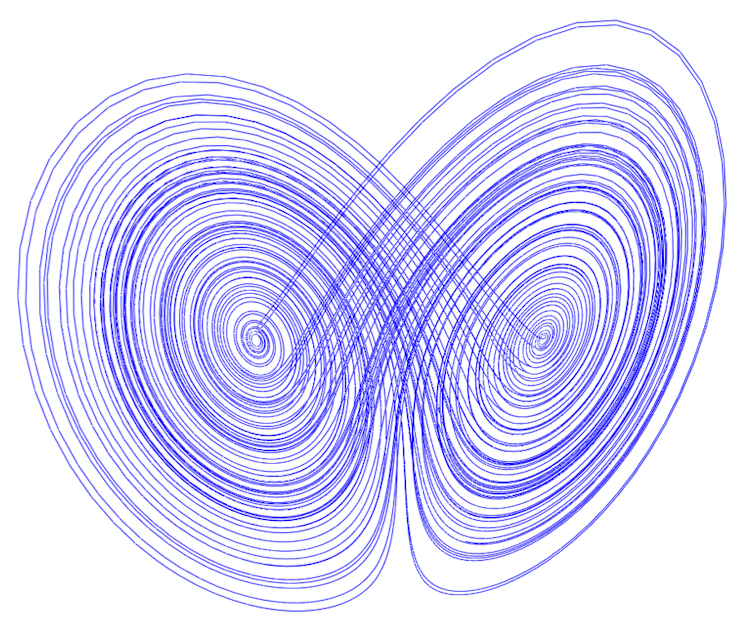
Although it is hard to predict individual trajectories, the Lorenz attractor shows that the system follows a general pattern. In real life, this is much like knowing that the four seasons will appear in the correct order, even if we can’t make specific predictions about next month’s weather.
Even so, it is useful to know what’s around the corner. To improve short-term forecasts, weather agencies are now turning to “ensemble predictions”. Rather than running a single simulation, forecasters use observed data to construct a variety of plausible starting conditions, then see what patterns these would lead to.
The ensemble method produces a collection of different scenarios, each of which could occur with a certain probability. Whereas weather simulations are generally only reliable 3-5 days into the future, ensemble methods can generate useful probabilities 7-10 days in advance.
Fast and unpredictable
Predicting normal weather is hard enough, but tornadoes are particularly elusive. Because they are such specific, localised events, they are highly sensitive to initial conditions. Although tornadoes usually emerge from “supercells” – thunderstorms that contain a large, rotating column of air – less than 30% of supercells lead to tornadoes. And there is no easy way to tell which will and which won’t.
While mathematical models can help forecasters anticipate conditions that might eventually result in a tornado, current warning announcements are based mainly on observations. As Lorenz found during his time in the Pacific Ocean, good data are crucial when making predictions. Weather agencies therefore analyse information from weather stations, radar, satellites, weather balloons, as well as a volunteer network of storm spotters.
To improve warnings, researchers at the U.S. National Severe Storms Laboratory are now looking at ways to make ensemble predictions about tornadoes over short timescales. Taking advantage of boosted computing power and better information – such as high-resolution radar data – these so-called “warn-on-forecasts” aim to increase the present warning lead-time, which stands at 13 minutes on average.
The inherent unpredictability of tornadoes means that improved forecasts might still be limited to a matter of hours. But in a situation where every minute counts, that could make all the difference.

