Dans la mythologie grecque, Chaos est l’élément primordial de la théogonie hésiodique, où il désigne une profondeur béante. Ovide en fait dans ses Métamorphoses une « masse informe et confuse qui n’était encore rien que poids inerte, amas en un même tout de germes disparates des éléments des choses, sans lien entre eux ». Dans la tradition judéo-chrétienne, le chaos est un état vague et vide de la terre avant l’intervention créatrice de Dieu. Aujourd’hui, dans le langage courant, il représente un état de confusion générale, de désordre, de perturbation.
En mathématiques, le concept de « théorie du chaos » a un sens plus spécifique. Cette discipline étudie le comportement des systèmes dynamiques, systèmes qui évoluent avec le temps, très sensibles aux conditions initiales. Ainsi, des différences infimes dans les conditions initiales entraînent des évolutions totalement différentes, rendant toute prédiction impossible ou difficile à long terme. La théorie du chaos a de nombreuses applications : météorologie, sociologie, physique, informatique, ingénierie, économie, biologie et philosophie.
C’est en voulant prédire le temps qu’il fait grâce à des équations déterministes de la physique que la théorie du chaos est née. Et l’image que l’on en a, popularisée notamment par le film Jurassic Park, est celle du battement d’ailes de papillon capable de provoquer une tornade ailleurs sur le globe.
L’effet « papillon »
Bien que le caractère vraisemblablement chaotique de la météorologie fut pressenti par Henri Poincaré, le météorologue Edward Lorenz est néanmoins considéré comme étant le premier à le mettre en évidence, en 1963. La météo est le système dynamique par excellence, prédire le « temps » qu’il fera est un vrai défi. Si on tente de le relever, il faut modéliser le climat à l’aide des équations très compliquées et très lourdes, tirées de la mécanique des fluides et thermodynamique essentiellement. Néanmoins, Lorenz réussit à considérablement simplifier ces équations.
Puis, il décide de faire appel au meilleur ordinateur de son époque pour mener à bien la résolution de ces équations. Il démarre ses équations à partir des « conditions initiales » (valeurs des paramètres des équations à t=0, le début). Il arrête sa simulation, puis la relance en modifiant les conditions initiales : au lieu de reprendre les valeurs de t=0, il prend des données choisies à un autre instant t de sa précédente simulation. Pour Lorenz, cette nouvelle simulation devait être identique à la partie de la simulation précédente qui suivait la valeur t choisie comme condition initiale pour la nouvelle. Or, à sa grande surprise, même si les trajectoires commencent bien de façon identique, elles finissent par se séparer et évoluer de façon complètement différente ! Les paramètres initiaux t ont donc une influence sur l’évolution du système entier.
En réalité, tout est une question de chiffres « significatifs », qui indiquent la précision d’un calcul. Par exemple, 4,54 (3 chiffres significatifs) est moins précis que 4,54007 (6 chiffres significatifs). Or, lors de sa seconde simulation, Lorentz avait utilisé non pas la valeur précise de t (avec 6 chiffres significatifs), mais une version arrondie (3 chiffres significatifs seulement), pensant que le faible écart serait insignifiant. Or, ce n’est pas le cas ! On comprend alors son étonnement face à cette évolution.
En 1972, Lorenz fait une conférence à l’American Association for the Advancement of Science, intitulée : « Prédictibilité : le battement d’ailes d’un papillon au Brésil provoque-t-il une tornade au Texas ? », à l’origine de « l’effet papillon ». Pourtant, bien sûr, ce n’est pas un papillon qui cause la tornade : elle serait causée par l’ensemble de l’historique des changements météorologiques. Vu que tous les plus infimes détails comptent de par l’extrême sensibilité aux conditions initiales, c’est l’ensemble de ces paramètres qui va potentiellement créer une tornade. Cette complexité vient donc annihiler toute velléité de prédiction météorologique à long terme. Rappelons également que le modèle de Lorentz est très simplifié, et qu’il est pourtant sujet au comportement chaotique : l’effet est plus important encore avec des modèles plus réalistes et donc plus complexes.
Attracteur étrange
On peut d’ailleurs avoir des comportements chaotiques pour des modèles encore plus simples. C’est par exemple le cas de la fonction logistique (aussi appelée Modèle de Verhulst, elle modélise la croissance d’une population animale en dynamique des populations). Vous prenez un nombre x compris entre 0 et 1. Vous retranchez ce nombre à 1 (1-x). Vous multipliez ce nombre par le nombre de départ (soit x(1-x)) et vous multipliez encore le tout par n’importe quel nombre positif a (soit ax(1-x)). Faites cette opération autant de fois que vous voulez : chaque étape sera appelée itération.
Vous ne le soupçonnez peut-être pas, mais la valeur de ce nombre « a » va révéler la nature chaotique de cette opération. Si a est compris entre 0 et 1, au bout de quelques itérations, vous trouverez la valeur 0. Si a est compris entre 1 et 3, vous convergerez vers un nombre, jamais le même, mais un nombre seul (en fait, on peut montrer que l’on converge vers une valeur (a-1)/a). Puis, lorsque a est compris entre 3 et 3,45 vous trouverez au bout d’un certain nombre d’itérations que le résultat oscille entre deux valeurs de manière périodique. Entre 3,45 et 3,54, c’est autour de 4 valeurs, au-delà de 3,54 c’est 8 valeurs, etc.
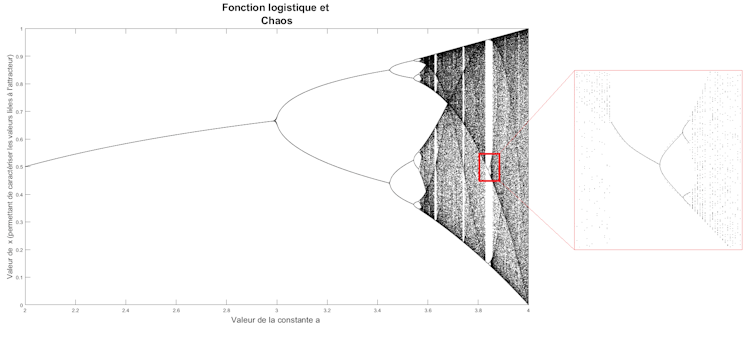
On obtient ainsi une succession de bifurcations entre les comportements périodiques et le chaos. Cette succession de bifurcation correspondant à la « mise en place » d’une complexité qui se matérialise en chaos en fonction de la nature de l’attracteur. C’est ce que l’on observe pour a=3, une bifurcation vers 2 valeurs (comportement périodique), puis pour a=3,45 deux bifurcations vers 4 valeurs, etc. De bifurcation en bifurcation, les évolutions deviennent de plus en plus complexes. Le processus aboutit, pour a > 3,57 environ, à des systèmes qui ne présentent généralement plus d’attracteurs visibles. Les graphiques représentent alors une évolution « chaotique » au sens usuel du terme.
On comprend alors l’importance de la notion d’attracteur : un point, une droite ou un espace vers lequel le système évolue de façon irréversible sans perturbations extérieures. Ainsi, la fonction logistique possède :
un attracteur ponctuel fixe lorsque a est compris entre 0 et 3 ;
un attracteur possédant une « orbite » périodique pour a compris entre 3 et 3,45 ;
un attracteur chaotique dit « étrange » car possédant une structure fractale pour a au-delà de 3,45.
Concernant l’aspect chaotique, l’attracteur étrange n’est ni une courbe, ni une surface, mais un objet fractal, c’est-à-dire un objet qui se répète à l’infini. En zoomant sur une partie, le tout refait son apparition. Il y a « autosimilarité » à toutes les échelles, c’est-à-dire que le même objet est observable même en augmentant l’échelle. On peut l’observer sur le diagramme ci-dessus : par endroit, il y a des bandes blanches qui contiennent les mêmes bifurcations observées au départ. Cela nous donnerait presque l’impression de comprendre une « mécanique du chaos »…
Mais revenons au système de Lorenz. Lorsque les 3 paramètres du modèle prennent certaines valeurs, le système dynamique de Lorenz présente un attracteur étrange en forme d’ailes de papillon. Pour presque toutes les conditions initiales choisies par Lorenz, l’orbite du système (c’est-à-dire les trajectoires décrivant toutes les valeurs calculées associées au modèle) s’approche rapidement de l’attracteur, la trajectoire commençant par s’enrouler sur une aile, puis sautant d’une aile à l’autre pour commencer à s’enrouler sur l’autre aile, et ainsi de suite, de façon apparemment erratique.

L’existence d’un attracteur étrange pour certaines valeurs des paramètres a été conjecturée par Edward Lorenz dès 1963 sur la base de simulations numériques. Il a cependant fallu attendre 2001 pour en avoir une démonstration rigoureuse par Warwick Tucker. D’autres modèles et leurs attracteurs étranges correspondants existent, mettant ainsi en évidence la profondeur et l’exactitude de la théorie du chaos.
Le 20ᵉ siècle en sciences ou la fin tragique du déterminisme
Est-ce que la théorie du chaos a été inventée dans les années 1970 ? Oui et non. Le chaos avait en fait été déjà envisagé, notamment par Poincaré, qui s’était déjà posé la question de la stabilité du Système solaire. Il a ainsi pu montrer que 3 corps en interaction gravitationnelle sont susceptibles d’être instables. Cependant, pour la communauté scientifique de l’époque, renoncer au déterminisme en sciences s’est avéré trop compliqué.
Finalement, avec la physique quantique et le théorème d’incomplétude de Gödel, la théorie du chaos précipite la chute du déterminisme en sciences. « Un comportement complexe implique des causes complexes », pensait-on. Un dispositif mécanique, un circuit électrique, une population animale, l’écoulement d’un fluide, un organe biologique, un faisceau de particules, un orage, une économie nationale – bref un système qui était visiblement instable, imprévisible ou incontrôlé devait soit être régi par une multitude de composantes indépendantes, soit être soumis à des influences extérieures aléatoires.
Depuis Lorenz, les physiciens, mathématiciens, biologistes et astronomes ont créé de nouveaux concepts, une révolution en fait. Des systèmes simples peuvent engendrer un comportement complexe et des systèmes complexes, un comportement simple.
Théorie du « désordre » ou de la « complexité », il semblerait que là où commence le chaos s’arrête la vision « classique » de la science. Le « chaos » étant devenu objet d’étude, on croit (souvent à tort) le voir partout : des volutes d’une fumée de cigarette au mouvement de l’air lors d’un vol d’avion ; des bouchons sur une autoroute aux écoulements de pétrole dans les pipelines…
Le chaos efface les frontières entre disciplines. Théorie transdisciplinaire ou science de la nature globale des systèmes, le chaos est un vrai défi en termes de méthodologie scientifique. Le chaos élimine l’utopie d’une prédictibilité déterministe, mais questionne l’apparition d’un « ordre » dans une complexité peut-être apparente.

