Belajar berhitung dianggap paling sulit sehingga ada semacam fobia terhadap matematika di kalangan siswa sekolah dasar. Mereka merasa sulit memahami materi, tak bersemangat belajar, dan akhirnya berpengaruh pada prestasi belajar.
Para guru yang saya interview untuk riset pembelajaran matematika di sejumlah sekolah dasar negeri di Kecamatan Cisauk, Tangerang, Jawa Barat, pada 2015 mengatakan siswa mereka tetap mengalami kesulitan dalam memahami konsep matematika walau mereka telah mengulang materi pelajaran tersebut berkali-kali. Selain itu, siswa sering kali kurang beruntung dalam kompetisi matematika yang diadakan setiap tahun di kecamatan tersebut.
Memang, literasi matematika dasar siswa di Indonesia menjadi masalah besar hingga saat ini. Menurut hasil survei Programme for International Student Assessment (PISA), mayoritas siswa Indonesia (usia sekitar 15 tahun) hanya dapat menyelesaikan soal matematika di bawah level dua. Pada level dua, kemampuan siswa adalah mampu menyelesaikan soal hanya dengan satu cara/metode. Menurut PISA Level, tingkat tertinggi adalah level enam.
Lebih mengkhawatirkan lagi, riset Lant Pritchett, guru besar ekonomi pembangunan Universitas Harvard dan peneliti Center for Global Development Amerika Serikat, menyatakan diperlukan 317 tahun oleh anak Indonesia untuk menyamai tingkat kecanggihan berpikir rata-rata anak negara anggota Organisasi Kerja Sama Ekonomi dan Pembangunan (OECD) pada 2012. Riset Lant menggunakan data PISA dari 2000 sampai 2012.
Salah satu masalahnya adalah model pembelajaran berhitung yang saat ini digunakan di banyak sekolah dasar (SD) hanya mengajarkan metode konvensional atau vertikal yang cenderung mengajarkan logika terstruktur saja. Metode ini mengajarkan operasi penjumlahan, pengurangan, perkalian dan pembagian dengan susunan angka vertikal (dari atas ke bawah).
Selain metode vertikal, ada juga metode lain seperti metode jarimatika dengan bantuan jari tangan, atau sempoa dengan bantuan manik-manik ala Cina. Dua metode terakhir ini tidak menggunakan simbol matematika sebagai penjelasannya.
Read more: Pengajaran aritmatika di SD sembunyikan logika, bagaimana mengatasinya?
Metode yang tidak menggunakan simbol matematika berimplikasi pada ketidakmampuan siswa dalam membuktikan kebenaran hasil perhitungan melalui proses hitung matematika yang telah diakui secara internasional.
Dalam 19 tahun terakhir, saya mengembangkan Metode Horizontal (Metris) sebagai metode alternatif untuk memahami operasi penjumlahan, pengurangan, perkalian dan pembagian untuk siswa sekolah dasar. Metode perhitungan mendatar (dari kanan ke kiri) bisa diajarkan guru untuk memperkaya cara menyelesaikan soal selain metode vertikal dan untuk mengurangi fobia anak pada matematika.
Model Horizontal/Mendatar
Riset saya sendiri dan kolega serta penelitian dari Universitas Pendidikan Indonesia di Kota Cimahi menunjukkan bahwa metode hitung horizontal ini dapat digunakan sebagai metode pendukung untuk meningkatkan pemahaman siswa dalam pembelajaran matematika, terutama aritmatika SD.
Dalam riset dengan uji coba kelas dua sekolah dasar di Kota Cimahi, siswa terlihat belajar dengan aktif dan gembira karena tertarik pada metode ini. Setelah diajarkan oleh guru, mereka mencoba sendiri metode tersebut dan antusiasme ini diyakini akan meningkatkan daya pikir dan pemahaman siswa dalam operasi pada bilangan.
Metode Horizontal mempunyai cara yang unik dalam proses perhitungan aritmatika dasar seperti penjumlahan, pengurangan, perkalian, dan pembagian. Dalam proses hitungan, metode ini menggunakan notasi pagar yang ditulis secara mendatar (horizontal) dari kanan ke kiri.
Notasi pagar metris
Notasi adalah representasi dari suatu ide dan konsep mempunyai arti (meaning) yang akurat. Agar Metode Horizontal dapat mengembangkan konsepnya dengan akurat, maka diperkenalkan Notasi Pagar, yang disimbolkan dalam bentuk tanda | untuk merepresentasikan Konsep Asosiasi Posisi.
Konsep Asosiasi Posisi atau disebut juga Nilai Tempat (place value) satuan, puluhan, ratusan, ribuan, puluhan ribu, ratusan ribu dan seterusnya merupakan landasan dari Bilangan Desimal yang dikonstruksi dari digit-digit mulai dari nol hingga sembilan.
Contoh cara mengkonversi bilangan desimal biasa menjadi bilangan desimal dengan notasi pagar, seperti bilangan 234 = 2|3|4.
Konversi dari bilangan notasi pagar ke desimal
Untuk “mengkonversi balik” dari bilangan notasi pagar menjadi bilangan desimal, perlu diingat aturan dasar untuk notasi pagar, yaitu jumlah digit bilangan di sebelah kanan notasi pagar harus sama dengan jumlah notasi pagar.
Contoh 3|2|5 = 325.
Bila jumlah digit bilangan di sebelah kanan notasi pagar lebih sedikit dari notasi pagar, maka disisipkan bilangan Nol (0) di depan bilangan agar jumlah digit bilangan di sebelah kanan notasi pagar sama dengan jumlah notasi pagar.
Misalnya untuk penulisan 205 bisa ditulis dengan: 2||5 = 2||05 = 205.
Sedangkan bila jumlah digit bilangan di sebelah kanan notasi pagar lebih banyak dari notasi pagar, maka harus ada bilangan yang dipindah dan dijumlahkan dengan bilangan yang terletak di sebelah kiri notasi pagar.
Untuk soal 60 + 25 = (6|0) + 25 bisa dikerjakan dengan cara: 6|25 = 6+2|5 = 8|5 = 85.
Prinsip persamaan tanda
Dalam Metris, agar bentuk Notasi Pagar dapat dikembalikan menjadi bentuk desimal biasa harus menggunakan prinsip persamaan tanda. Apabila terdapat Kolom yang mempunyai tanda (+/-) yang berbeda dengan kolom yang lain, maka lakukan langkah-langkah berikut:
A. Jika tanda pada kolom paling kiri positif, maka buat semua kolom yang lain bertanda positif juga.
Jadi untuk soal 30 - 3 = (3|0) - 3 bisa diselesaikan dengan:
3|-3 = 3-1|10-3 = 2|7 = 27.
B. Jika tanda pada kolom paling kiri negatif, maka buat semua kolom yang lain bertanda negatif juga.
Untuk soal -50 + 4 = (-5|0) + 4 menjadi:
-5|4 = -5+1|4-10 = -4|-6 = -46.
Penjumlahan dua metode
Contoh Metode Horizontal yang paling sederhana dalam penjumlahan dua bilangan:
ab + cd = a+c|b+d
Penjumlahan di atas dalam bentuk angka dalam Metode Horizontal, misalnya:
87+96 = (8|7)+(9|6) = 8+9|7+6 = 17|13 = 17+1|3 = 18|3 = 183
Sebagai perbandingan, dapat dilihat di bawah ini penyelesaian dengan Metode Vertikal dengan hasil akhir yang sama:
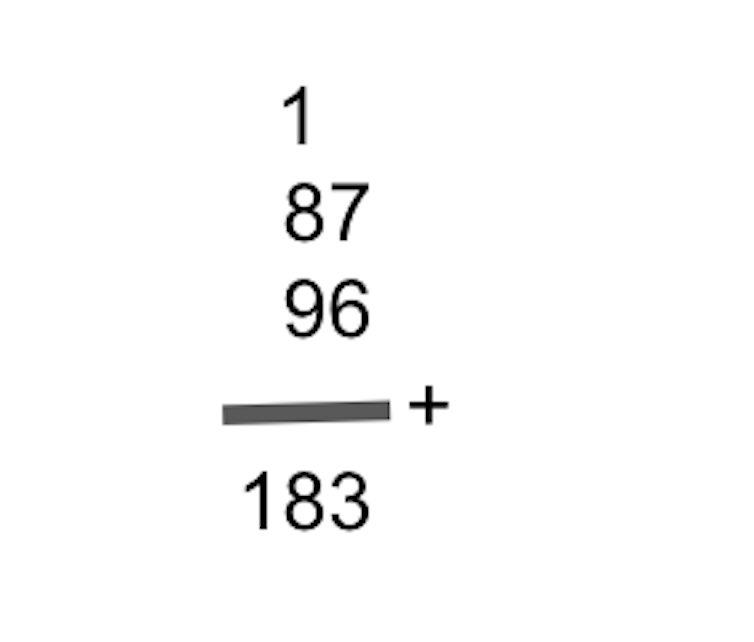
Bila dicermati penyelesaian soal di atas dengan Metode Vertikal maka perlu ada angka yang disimpan (dalam kasus ini angka 1). Penyimpanan angka yang terus menerus ini menyebabkan daya tahan otak siswa dapat cepat lelah sehingga probabilitas kesalahan perhitungan juga dapat meningkat.
Atasi fobia
Fobia anak-anak terhadap matematika dasar dapat muncul karena salah persepsi bahwa perhitungan dengan bilangan seperti penjumlahan yang makin besar (puluhan, ratusan, ribuan) akan makin sulit.
Hal ini terjadi karena kemampuan visual anak terhadap bilangan umumnya maksimal 20 angka sesuai dengan banyaknya jumlah jari tangan dan kaki mereka. Fobia itu mungkin dapat terjadi dalam pembelajaran metode konvensional/vertikal.
Pembelajaran Metris memberikan cara berpikir yang berbeda. Syarat bagi anak untuk mahir berhitung dalam penjumlahan dengan bilangan puluhan, ratusan bahkan ribuan, anak cukup menguasai penjumlahan satuan saja alias maksimal bilangan 9+9=18 yang mampu divisualisasi oleh jumlah jari mereka. Dalam Metris, bilangan yang besar dapat dicacah ke dalam bentuk angka-angka satuan.
Pada akhirnya menyelesaikan soal matematika dengan metode alternatif, apalagi dengan metode baru, tetap butuh kerja keras dan latihan berulang-ulang. Guru berperan penting dalam proses ini.