How many people do you have to put into a room before you are guaranteed that at least two of them share a birthday?
We all know and love the blissful feeling of winning an argument. Well, trust me, that’s an even better feeling if you’re a mathematician.
It’s not a matter of finding the right words – rather it’s the right ideas applied in a rigorous manner. And when this is done properly, the winner of the argument becomes known to everyone in the room.

The loser skulks back to his place of study, bloodied and bruised, to lick his or her wounds. What had seemed intuitively right is cancelled by a couple of lines of mathematics scrawled on the back of an envelope.
Maybe that’s why mathematicians live in harmony, at least most of the time. We understand that belief and intuition can guide us towards a result, but these are not vessels capable of delivering final proof.
The Monty Hall Problem, which I wrote about recently, is a fine example of simple mathematics defying general intuition. And when I say defying, I really mean guiding: every time we are subject to such a striking idea our intuition actually aligns itself just that little bit more with reality.
In the spirit of sharing more paradigm-shifting mathematical delights with you all, we will consider another problem which will hopefully tug your belief system that little bit more.
A simple question
So, again:
how many people do you have to put into a room before you are guaranteed that at least two of them share a birthday?

The solution is fairly simple; there are 366 possible days (damn those leap years) that somebody can be born on. So if you had 367 people in a room, there’s no way to assign each of them a birthday without having to use a date more than once.
The above idea is known to mathematicians as the pigeonhole principle: if you have to sort items into pigeonholes, and there are more items than pigeonholes, then at least one pigeonhole has to contain more than one item.
The same principle lends itself to proving statements such as “in Sydney there will be at least two people with the same number of hairs on their head”.
A less simple question
Have a think about the following related problem:
How many people do you have to put into a room before you have a more than 50% chance that at least two of them share a birthday?
Most people guess 184, as this is a bit more than half of 366.
But the correct answer is actually 23. If you throw 23 randomly selected people into a room then it’s more likely than not that two of them share a birthday.
I’ve never seen anybody ballpark this number, or anything remotely close to it. It’s a counterintuitive result. Of course, I’m hoping that I can convince you with the following argument (calculators out, please).
The dirty details
Let’s make an assumption for simplicity, but this won’t void the argument. Just consider a regular year of 365 days and assume that all 365 birthdays are equally likely.
Sure, it’s known that in reality the birthdays of the population are subject to some variation but that’s OK – any sort of irregularities in reality would only increase the chances of a shared birthday.
So, we have a room of 23 people. We will actually calculate the probability that they all have different birthdays and show that this is less than 50%.
We walk in to our room, grab a person – Frank – and put him to the side. We then choose another person, Betty. The probability that Betty has a different birthday to Frank is 364/365, as there are 364 days in the year that Frank was not born on.
We then grab another person – Shazza – and bring her over to the side. There is a 363/365 probability Shazza doesn’t share a birthday with Frank and Betty, as there are 363 remaining days their birthday could fall on.

If we keep doing this, bringing a person over and calculating the probability that they don’t share a birthday with the group before adding them to the group, we generate a bunch of probabilities:
364/365, 363/365, 362/365, … , 344/365, 343/365
The first probability arose from demanding that Frank and Betty do not share birthdays. The second probability has that Shazza doesn’t share a birthday with Frank or Betty. The probabilities continue in this way.
If we wanted to know the overall probability – that is, the probability that no two people share a birthday – we need to multiply together all of the above probabilities. In doing so we get that there is a 49.27% that none of them share a birthday, and this means that there is a 50.73% chance that at least two of them share a birthday!
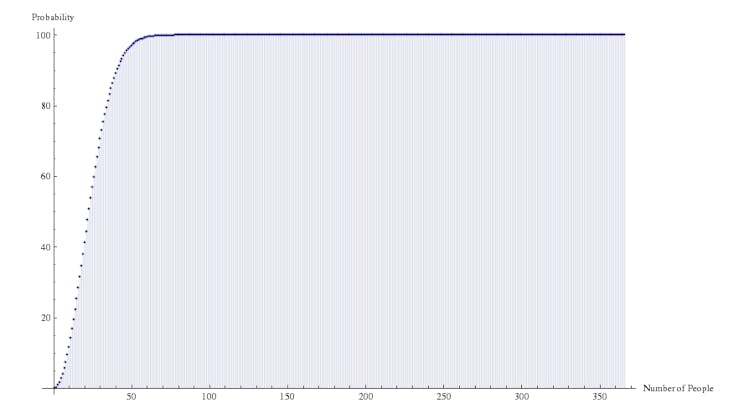
You can have a go at repeating the calculation for numbers other than 23. In particular, you can prove that 22 people isn’t enough for a more than 50% chance. Also, 57 people will give you a 99% chance of a shared birthday!
Here’s a graph that shows the probability of a shared birthday given different numbers of people in a room.
And if you happen to be celebrating your birthday today, many happy returns.

