Après de brillantes études, vous avez été recruté au ministère des Affaires étrangères. Un jour le ministre vous convoque pour vous annoncer la bonne nouvelle : ça y est, il a enfin réussi à convaincre ses homologues de 100 pays à envoyer des ambassadeurs à Paris dans une semaine pour un congrès sur la paix et les échanges culturels. Maintenant c’est à vous d’organiser tout ça. Ce colloque lui tient vraiment à cœur. Il faut que ça soit une réussite, il en va de l’honneur du pays !
Après d’âpres négociations, 30 thèmes ont été retenus. Cet évènement se déroulera sur une seule journée et sera organisé sous forme de réunions d’une heure chacune, dont les noms de code sont R1… R30. Les participants à chaque réunion sont fixés, vous avez la liste. Le ministère a loué un espace avec 30 salles suffisamment grandes pour accueillir tous les participants.
Le ministre s’exclame : « Grâce aux 30 salles de réunions, tout cela va pouvoir se boucler en une seule heure. Ça donnera ensuite aux délégations l’occasion de se rencontrer de manière informelle pour discuter. Excellent, tout ça ! » Visiblement le « patron » n’a pas tout en tête. Vous lui glissez : « M. le ministre, cela ne va pas pouvoir se faire exactement comme vous dites. Par exemple, il est prévu que le diplomate canadien assiste à trois réunions. Il n’est donc pas possible de mettre les 30 réunions toutes en même temps sinon il ne pourra assister qu’à une seule. » Après un instant de réflexion, le ministre vous dit : « En effet… Je vous confie la mission d’établir le planning. » Avant que vous n’ayez pu émettre un son, il a déjà tourné les talons, préoccupé par les déclarations qu’il devra faire devant la presse. L’organisation n’est pas son problème ; c’est le vôtre.
Vous vous mettez à l’œuvre immédiatement. Vous prenez une feuille de papier : vous y dessinez 30 ronds, chacun représentant une réunion. Ensuite, vous tracez un trait entre deux réunions Ri et Rj si elles ont un ou plusieurs participants en commun et ne peuvent donc pas avoir lieu en même temps (sinon ces personnes inscrites à Ri et à Rj ne pourront pas suivre les deux, ce qui peut provoquer une crise). Ce que vous obtenez est un graphe. Les réunions sont les éléments ou sommets du graphe. Un trait éventuel entre deux sommets est une arête.
Read more: La vie secrète des graphes
Pour commencer à tâter le terrain, examinons deux cas extrêmes.
Graphe sans arête : les réunions peuvent être organisées toutes en même temps (chaque participant n’assiste qu’à une réunion). En une seule heure, tout est terminé.
Graphe complet : entre chaque paire de sommets, il y a une arête. Dans ce cas il faut prévoir 30 réunions successives car aucune ne peut avoir lieu en même temps qu’une autre. Durée totale : 30 heures !
En regardant votre dessin, vous constatez que vous n’êtes ni dans un cas ni dans l’autre. Les choses ne vont pas être simples…
Coloration de graphes
Ce que vous avez à faire s’appelle de la coloration de graphe. Une coloration de G est la donnée d’une couleur (ou un entier qui représente la couleur) à chaque sommet de telle manière que si deux sommets sont reliés par une arête (on dit qu’ils sont voisins) alors ils ne doivent pas avoir la même couleur.
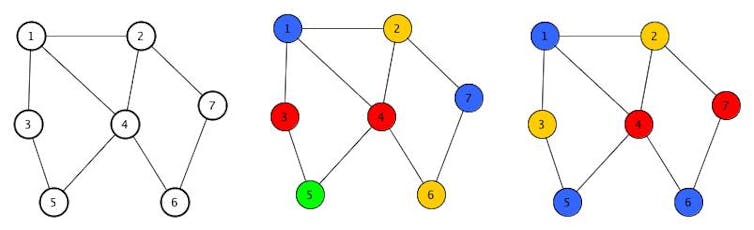
Observons les trois graphes ; celui non coloré le plus à gauche ; à sa droite une coloration utilisant 4 couleurs ; enfin une coloration qui n’utilise que 3 couleurs. Posons le problème suivant : étant donné un graphe G quelconque, construire une coloration de G utilisant le nombre minimum de couleurs, dite coloration optimale.
Notez que les couleurs utilisées n’ont pas d’importance, seul compte le nombre total de couleurs utilisées.
Sur l’exemple de la figure 1, la coloration la plus à droite est optimale (impossible de colorier ce graphe avec moins de 3 couleurs) et permet de faire les 7 réunions en seulement 3 heures (une couleur = un créneau d’une heure). Notez qu’il peut y avoir plusieurs colorations optimales. Par exemple le sommet 6 pourrait être colorié en jaune (au lieu de bleu).
Mais au fait, comment a-t-on trouvé cette solution ? Vous avez consulté un livre sur les graphes et vous vous êtes rendu compte que votre problème fait partie de la liste des problèmes algorithmiques les plus difficiles (il est lié à ce que l’on appelle la question « P=NP ? »). En faisant quelques estimations, vous vous apercevez qu’avec une méthode exacte il vous faudra largement plus d’une semaine pour calculer une coloration optimale, même en utilisant l’ordinateur le plus puissant du ministère. Vous le sentez bien : tout cela ne va pas plaire au ministre si vous lui donnez le planning de l’évènement… après l’événement lui même.
Comment faire alors ? Il n’y a pas de méthode totalement satisfaisante pour résoudre ce type de problèmes. Soit vous voulez une réponse exacte et dans ce cas vous allez devoir calculer très, très, très longtemps, soit vous voulez « rapidement » une réponse et dans ce cas vous risquez d’avoir une réponse de qualité médiocre. Il faut souvent faire des compromis entre temps de calcul et qualité du résultat.
Une approche simple et gloutonne
Allons-y pour un travail à la pelle. Un algorithme très simple à mettre en œuvre est à votre disposition. Voici comment il marche sur un exemple de la figure ci-dessous.
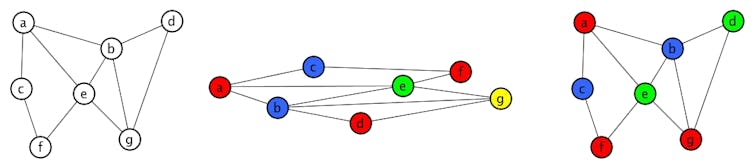
Considérons une liste des sommets de ce graphe. Pour faire simple, prenons la liste a, b, c, d, e, f, g. Définissons maintenant une liste de couleurs numérotées : 1 est rouge ; 2 est bleu ; 3 est vert ; 4 est jaune ; 5 est orange. Précisons que seul compte le numéro de la couleur, pas la teinte en elle-même. Le cœur de l’algorithme consiste à prendre chaque sommet, dans l’ordre de la liste (a, puis b puis c, etc.) et à le colorier avec une couleur de la liste avec la règle suivante : ce sommet reçoit la plus petite couleur non encore attribuée à ses voisins déjà coloriés. Pour illustrer, nous avons représenté le graphe en mettant les sommets de gauche à droite, dans l’ordre a, b, c, d, e, f, g.
Le sommet a, le premier de la liste, n’a aucun voisin déjà colorié. On lui donne donc la plus petite couleur de la liste : rouge. On passe au suivant, le sommet b, qui a maintenant un voisin déjà colorié (le sommet a). La plus petite couleur possible pour lui est alors bleu. Au tour de c qui n’a qu’un voisin déjà colorié : (a en rouge). Il prend alors lui aussi la couleur bleu. Le prochain sommet de la liste, d n’a qu’un voisin déjà colorié, b qui est en bleu. D’après la règle il prend alors la couleur la plus petite compatible avec cette contrainte, qui est rouge. Le sommet e a deux voisins coloriés, un en bleu, l’autre en rouge, il est donc obligé de prendre la 3e couleur, vert. Le sommet f a un voisin bleu et un vert. Il peut donc prendre la couleur rouge. A la fin, g doit obligatoirement prendre la 4e couleur de la liste, le jaune. Vous êtes un peu perdus ? Regardez donc la vidéo ci-dessous.
En appliquant cette méthode avec cette liste, quatre couleurs sont utilisées (le planning correspondant tient sur quatre heures en tout). La coloration du même graphe, la plus à droite n’utilise que trois couleurs (donnant un planning de trois heures seulement), ce qui montre bien, que, hélas, cette méthode ne retourne pas toujours une coloration optimale.
Il vous vient alors une idée : « Et si j’essayais toutes les listes ? » Pour chaque liste vous coloriez suivant la méthode précédente et vous gardez en mémoire celle qui a utilisé le moins de couleurs. Mais avec 30 sommets vous avez 265252859812191058636308480000000 listes à tester en tout (30 choix pour le 1er de la liste puis 29 pour le 2e, puis 28 pour le 3e, etc, ce qui donne en tout 30*29*28*… *2*1 listes). Même en en testant 10 000 000 000 par seconde avec un ordinateur puissant, il vous faudra environ 841 111 300 774 324 ans pour tout faire.
Le découragement vous gagne. Que va dire le ministre si vous lui apportez le planning dans 841 111 300 774 324 ans ? Il faut que vous trouviez une solution ! Il est impossible de tester toutes les listes mais rien ne vous empêche d’en essayer au hasard quelques milliers avec votre ordinateur. C’est ce que vous faites. Par chance, cette méthode vous donne une coloration utilisant 8 couleurs. En la reprenant à la main, en « bricolant », vous arrivez à réduire à 6 couleurs. Vous êtes sauvé ! L’événement durera 6 heures en tout. C’est acceptable. Fier de vous, vous portez le planning, fruit de vos longs efforts, au ministre.
En jetant un œil distrait à votre travail, il vous annonce qu’en fin de compte l’ambassadeur d’Italie ira assister à la réunion 7 à laquelle il n’était pas initialement prévu et que l’ambassadeur japonais n’ira pas à la réunion 14 pour laquelle il s’était inscrit. Malheur ! ça risque de tout changer !
Allez, vous vous êtes fait des frayeurs pour rien. Le fait que le Japonais n’aille pas à la réunion 14 n’est pas grave. Le planning peut être conservé tel quel (on libère une contrainte) mais l’Italien induit une nouvelle contrainte. Il devait assister initialement aux réunions 4,8 et 11. Il doit maintenant, en plus, assister à la réunion 7. Dans votre planning, les réunions 4, 8 et 11 n’ont pas lieu au même moment (au moins à cause de l’Italien). Mais la 7 pourrait avoir lieu en même temps que la 4, la 8 ou la 11. Vous regardez votre planning. Ouf ! Ce n’est pas le cas.
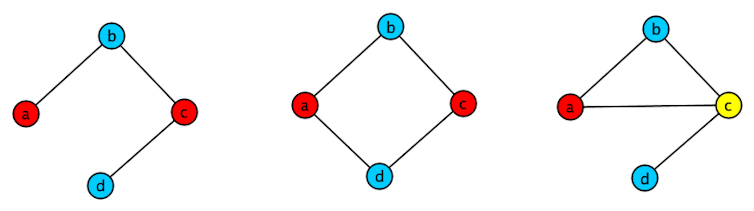
Observons sur un petit exemple ce qui peut se passer en cas de modifications des contraintes. Sur le graphe de la figure ci-dessous, le graphe le plus à gauche peut être colorié avec 2 couleurs. En ajoutant une arête entre a et d il est toujours possible de le colorier avec 2 couleurs. Par contre, en ajoutant une arête entre a et c, le « triangle » a,b,c créé nécessite l’utilisation d’une 3e couleur.
Happy end…
L’événement a eu beaucoup de succès. Le ministre est ravi et vous accorde quelques jours de congés au soleil, histoire de reprendre des couleurs, loin de celles des graphes !

