Compulsory maths for year 12 students! I’d like to see that – or would I?
There was much discussion recently about making it compulsory for year 12 students in NSW to study some mathematics. As a card-carrying mathematician, you might expect me to be very happy with such a suggestion. But, to the contrary, the suggestion has me frowning.
Already, across the country, 80% of Year 12 students are enrolled in some maths subject. Some may say that this is a very healthy number so what’s all the fuss about? Well good question.
Why study maths?
In the first instance we need to consider why 20% of students don’t study maths at Year 12.
Three reasons for students choosing any subjects at Year 12 spring to mind immediately; students like a subject, they are good at a subject or, they see a reason to study a subject.
Presumably for 20% of Year 12 students, at least one of these reasons fails to be true (or is less true about maths than it is for the subjects they do choose) and it’s hard to see what would be achieved by making maths compulsory for them.
Then there are students who leave school after Year 10. How do we improve their numeracy? Focusing on remediation in junior high school (and primary school) must be part of the discussion.
In February 2012, the Australian Mathematical Sciences Institute (AMSI) held a forum Maths for the future: Keep Australia Competitive that again highlighted the decline in maths participation and skills, showing the need for “intervention at multiple points on the educational pipeline”.
We need to think quite hard about what would be achieved by making Year 12 maths compulsory and how it might be done by way of curriculum design.
Make it relevant
Better ways (and definitely harder ways) to address the lack of maths participation for these students might include different teaching models, making clearer the importance of studying maths and making it relevant to a variety of areas of study.
Also increasing the number of skilled maths teachers in every maths class, not just senior maths classes, and developing curriculum models that have the capacity to reinforce concepts and remediate any misconceptions will have a significant, positive impact.
All of the above suggestions would benefit all students studying maths. The critical element to improving maths skills in students is surely the teacher in the room.
Teachers that count
Data from a Staff in Australia’s Schools study and used by the Australian Council for Educational Research (ACER) for 2010 show* around 40% of Year 7-10 and 24% of Year 11-12 maths teachers are teaching out of their field.
Furthermore, 15% of Year 7-10 and 9% of Year 11-12 maths teachers have studied only one year of tertiary maths, and 62% of Year 7-10 and 78% of Year 11-12 maths teachers have greater* than five years maths teaching experience.
Making maths compulsory certainly won’t fix that.
Calling for compulsory maths study in Year 12 entirely misses the point. The concern about the poor levels of maths skills of our high school students must surely be a concern about the maths skills of students who do study maths at Year 12 and beyond.
Over the past 10 years at least, although the total proportion of students studying Year 12 maths has remained stable at around 80%. The trend around the country has been for students studying maths to take lower levels of maths, as indicated in the table below.
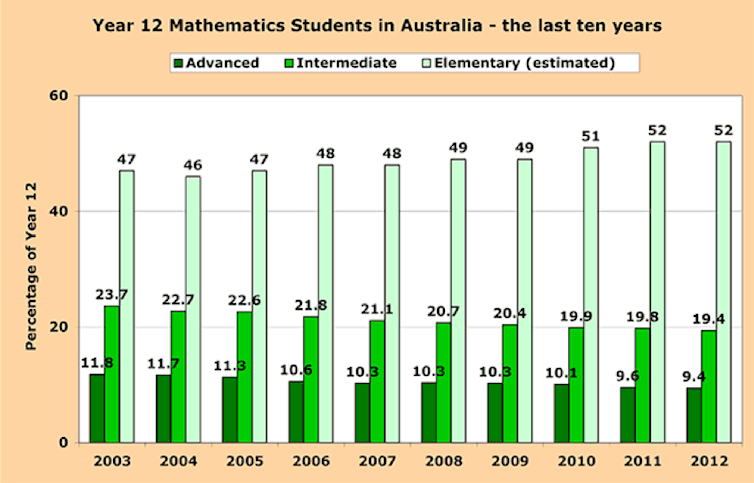
Assumed knowledge
There are a variety of reasons for this downward trend, and we in the tertiary sector, should acknowledge that we are in part responsible. Many Australian universities have removed hard prerequisites as entry requirements for engineering, science and commerce degree programs, opting instead for an assumed knowledge model.
But how do prospective students interpret that phrase and respond to it? In a recent ABC 7.30 Report story Australia’s Chief Scientist, Professor Ian Chubb, called on universities to tell students that maths is prerequisite for particular pathways of study. And for good reason.
When universities remove maths prerequisites from entry to degree programs for which mathematical knowledge is clearly needed, what message are we sending to schools and students about the importance of maths to these programs? Do we tell students what the consequences of not being adequately prepared in maths will be in relation to their pathways, retention and chance of success in their degree?
If we don’t (and I don’t think we do) why are we surprised when students make choices that will maximise their ATAR scores, since this is really what we are using as our selection instrument?
In June 2013, a workshop was held as part of the First Year in Maths project (funded by the Office of Learning and Teaching) where academics from around the country identified, overwhelmingly, that dealing with under-prepared students was their major challenge.
To date the project team has conducted 36 interviews with academics from around 22 universities across the country, and the picture emerging is that students don’t necessarily have the required assumed knowledge, sometimes far from it.
A solution?
This week academics and from across mathematics, science and engineering as well as peak education bodies with gather for a two day forum, Assumed knowledge in maths: Its broad impact on tertiary STEM programs. The aim is to obtain a clearer picture of the broad impact that the absence of maths prerequisites is having in science, technology, engineering and mathematics (STEM) programs.
An outcome of this forum could be an articulation of a baseline for maths preparation for students wishing to study tertiary level maths and science. Optimistically, this might also be nuanced in ways that catered for the various institutional differences and the particular requirements of the degree programs of universities across the country.
Whatever the outcome of this and other debates on the state of mathematics, the problem of declining maths skills is complex and its solution will not be easy, quick or as straightforward as making maths compulsory. But then nothing worthwhile is easily gained.
At the very least the solution will require qualified maths teachers in all maths classrooms, an engaging curriculum that has clear relevance to the multitude of pathways that students might pursue, including trades and business as well as science, and clear statements from the tertiary sector detailing the essential prerequisites that students require for their programs.
One goal might be to raise the level of maths skills for all students. Another might be that students choose to study the maths that they enjoy and is appropriate to their future careers.
Now I would like to see that.
* This article was amended to correct an error in the way some data was presented.

