The technology that allowed Marty McFly to travel back in time in the 1985 movie Back to the Future was the mythical flux capacitor, designed by inventor Doc Brown.
We’ve now developed our own kind of flux capacitor, as detailed recently in Physical Review Letters.
While we can’t send a DeLorean car back in time, we hope it will have important applications in communication technology and quantum computing.
How did we do it? Well it’s all to do with symmetry. There are many kinds of symmetry in science, including one that deals with time reversal.
Time reversal
Time reversal symmetry is a complex sort of symmetry that physicists like to think about, and relies on the imaginary as much as the real.
Suppose you make a movie of an event occurring. You could then ask: “If I edited the movie to run backwards, and showed it to my friends, could they tell?”
This might seem obvious: people don’t usually walk or talk backwards; spilt milk doesn’t spontaneously jump back into its carton; a golf ball doesn’t miraculously launch backwards from the fairway, landing perfectly balanced on the tee at the same moment as the club catches it.

But at a microscopic level, the story is not that clear. The collision of two billiard balls looks pretty similar in reverse; even more so for the collision of two atoms. A beam of light travelling in one direction obeys exactly the same laws of physics as a beam of light travelling in the opposite direction.
Indeed, the basic equations of physics look essentially the same if we replace time with its negative. This mathematical transformation reverses the flow of time in our equations.
Since the microscopic laws of physics appear to be unchanged under this mathematical transformation, we say the universe possesses time reversal symmetry, even though we cannot actually reverse time in reality. Unlike Doc Brown, we can’t make the clock tick backwards.
There is a conceptual conflict here. At the macroscopic scale, the entropy of the universe — a measure of disorder or randomness — always increases, so that there is an arrow of time.
This is obvious in our everyday experience: a scrambled egg is not reversible. How does this irreversiblity emerge from microscopic laws that are reversible? This remains a mystery.
The circulator circuit
Microscopic reversibility presents an important technological challenge. It complicates the diversion of electronic and radio signals around a circuit.
There are various applications where engineers want electromagnetic signals (such as light or radio waves) in a circuit to behave a bit like cars around a roundabout.
This is pictured below: a signal entering port A of the device should be directed to port B; a signal entering at B should go to port C; and a signal entering port C should be directed to port A, clockwise around the device.
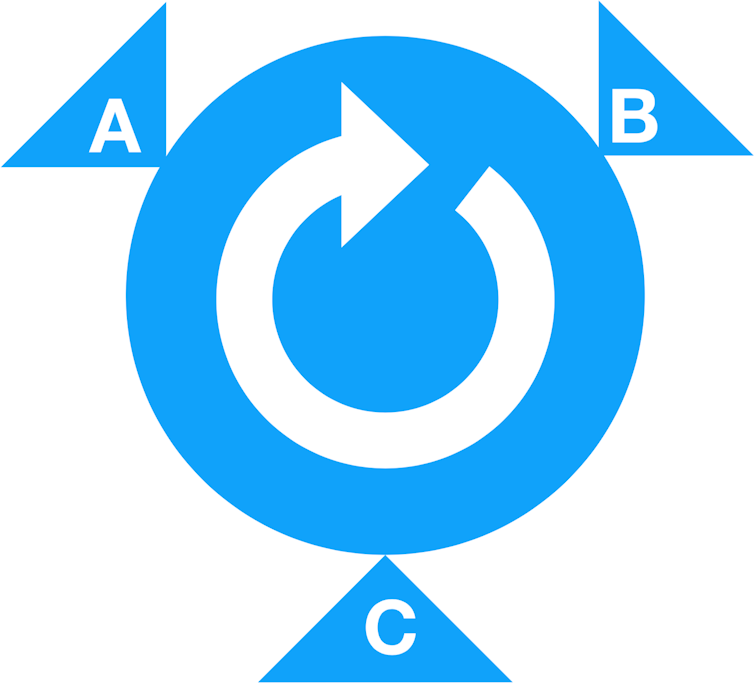
One way to do this is to use a network of amplifiers to switch signals as desired. But there is a profound result in quantum mechanics (the “no cloning theorem”) that means that amplification must always add noise, or randomness, to the signal. Sorry audiophiles: a perfect amplifier is impossible.
If the signal is extremely weak, so that additional noise is intolerable, then noiseless circulation is accomplished with a device called a circulator. Such devices are used to separate very weak signals going to and from sensitive electronics, including in radar receivers, or in existing and future quantum computers.
It turns out a device like this must locally break time reversal symmetry. If we made a movie of the signals coming and going from the circulator, and ran the movie backwards, it would look different. For example, we would see a signal entering port B and leaving via port A, rather than via C.
But most devices in a quantum research laboratory, such as mirrors, beam splitters, lasers, atoms do not break time reversal symmetry, so cannot be used as circulators. Something else is needed.
The practical way to break time reversal symmetry for real devices is to introduce a magnetic field. Like a rotating vortex in water, magnetic fields have a circulation, since they arise from electrical currents circulating in an electrical loop.
The magnetic field defines a direction of rotation (clockwise or counterclockwise) for electrically charged particles and thus for electrical signals. So when physicists say that a device breaks time reversal symmetry, they usually mean that there is a magnetic field about somewhere.
Commercial circulators are an anomaly in the world of electronics. Unlike transistors, diodes, capacitors and other circuit elements, basic materials science means that commercial circulators have not been miniaturised, and are still the size of a coin.

Building them into large-scale integrated microelectronic circuits is therefore a challenge. This will become an increasing problem as we try to fit thousands of qubits on a quantum computer chip, each requiring its own circulator to enable control and read-out.
Our quantum flux capacitor
We have developed a new way of building micrometer-sized circulators that can be fabricated on a microchip.
We figured out how to integrate magnetic flux quanta — the smallest units of magnetic field — with microfabricated capacitors and other superconducting circuit elements, so that time-reversal symmetry can be broken.
This led to our new circulator proposal. As with conventional circulators, there is a magnetic field present. But because we can use just one magnetic flux quantum, our design can be microscopic.
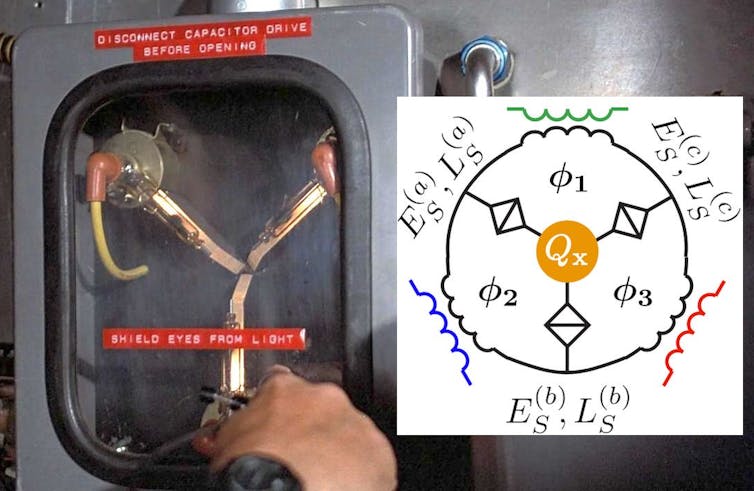
We’ve nicknamed the device the quantum flux capacitor as its circuit diagram has a passing resemblance to Doc Brown’s mythical invention (which are for sale, sort of).
Sadly for history buffs, our design won’t help much in your DeLorean time machine: it doesn’t reverse time. But its magnetic field does break time-reversal symmetry as advertised and we expect these devices will find applications in future quantum technologies.
Even sooner, they may help in high-bandwidth communications environments like mobile phone base stations in very dense populations, or for ultra-high sensitivity radar where every photon of the electromagnetic field counts.


