When you ask that question, three names come to mind: Roger Federer, Rafael Nadal and Novak Djokovic.
A simple way to compare tennis players is to look at how many grand slam tournaments they have won. That includes victories at the Australian Open, the French Open, Wimbledon in the UK and the US Open.
But this doesn’t take into account how many tournaments they’ve played, which tournaments they’ve played, how far they progressed in each tournament, and who they played against.

Probably the best player
My method estimates the probability of a player winning a match in a grand slam tournament. The player with the highest estimated probability of winning a match is then deemed the best player.
Using probability naturally accommodates how many matches and tournaments the player has played, and acknowledges the strong performance of a player who makes a final but doesn’t win the tournament.
The method builds a statistical model to estimate winning probabilities for each player from grand slam data.
By using a technique called regression modelling, it accounts for the fact the winning probability may depend on the quality of the opposition and the grand slam played. For example, some players have preference for hard courts (used at the Australian and US Opens) over clay (used at Roland Garros, home of the French Open).
The opposition quality is inferred from their ranking, and we consider five groups: the top 10, top 20, top 50, top 100 and outside the top 100. These group choices are consistent with terminology used by commentators and pundits.
Another advantage of using a statistical model is that we can make the most of the available data, which is quite small given there are only four grand slam tournaments per year.
For example, if the data support it, the model can enforce a similar pattern of performance against the quality of opposition across tournaments. This is a form of “borrowing of strength” to increase the accuracy of probability estimates from small datasets.

Oh, the uncertainty
Using a statistical approach allows us to quantify the uncertainty in probability estimates. Here we communicate uncertainty as an interval (lower and upper limit), that contains the true winning probability with a 95% chance.
So, for example, if the estimated winning probability for a player is 0.77 with an interval of 0.63 to 0.86, it means that our best guess of the winning probability is 0.77. But there is a 95% chance the actual winning probability is between 0.63 and 0.86. This tells us how much uncertainty there is about our best guess.
The amount of uncertainty depends on the number of matches played and the winning probability. There will naturally be more uncertainty if the actual winning probability is around 0.5, that means an even chance of winning or losing.
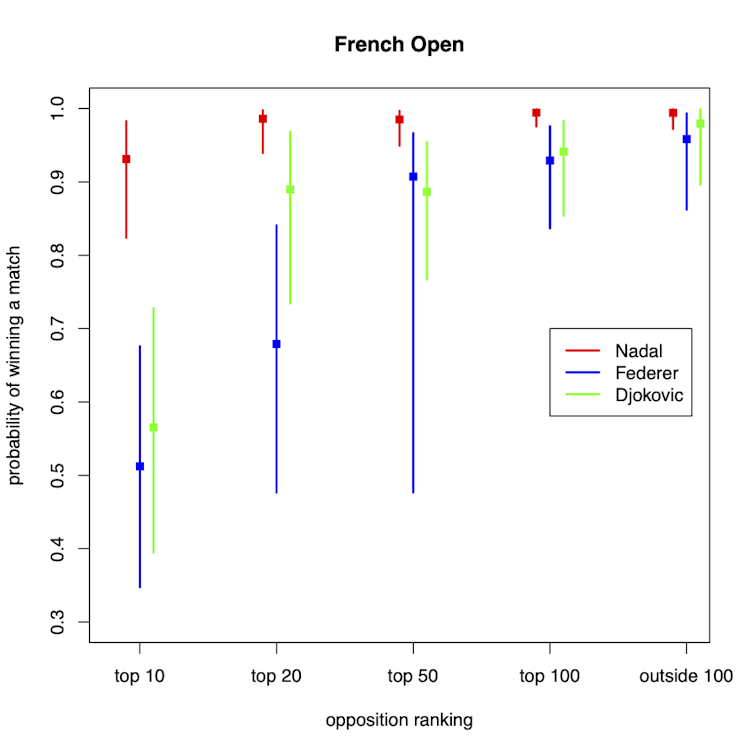
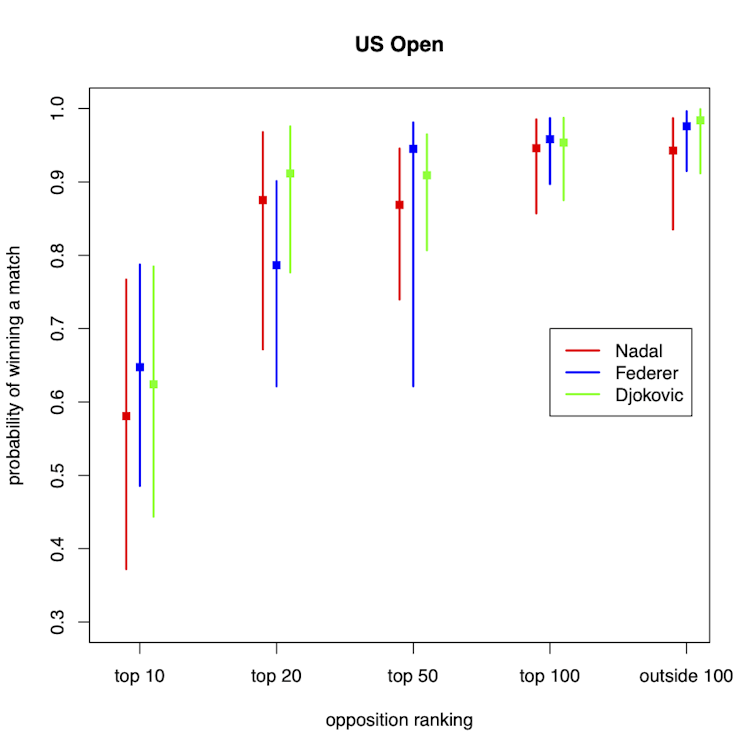
The results are shown in the figures (below). Each square represents the best probability estimate for Federer, Nadal and Djokovic, and the vertical line represents the uncertainty interval.


The winner is …
For the Australian Open, there is evidence to suggest that Djokovic is the top-performing male player.
But given the overlapping uncertainty intervals in the probability estimates with the other players, it is difficult to definitively state this.
It is difficult to separate the three players at the US Open. Wimbledon appears to be the tournament that Federer shines the most relative to the other players, but again there is significant overlap in the intervals.

Although there is some evidence that Nadal is the worst-performing player at the Australian Open and at Wimbledon (which is played on grass courts), he is the undisputed champion at the French Open.
Incredibly, Nadal has an estimated probability around 0.93 to win a game against a top 10 player at this tournament. This clearly shows Nadal’s dominance on clay courts. The French Open is a relative Achilles’ heel for Federer.
The analysis reveals some other interesting results. For example, the results suggest Nadal performs similarly against top 20 and top 50 players, as does Djokovic.
But there is generally a big drop in winning probability against top 10 players.
Apart from some cases (Nadal at the French Open, Djokovic at the Australian Open and Federer at Wimbledon), the chance that one of these champion players beats a top 10 player in a grand slam isn’t much better than a coin toss.
And the best player is …
On the women’s side, it’s widely accepted that Serena Williams is the top player in the modern era, and possibly of all time. Williams has won the most grand slams of any current player, male or female.
Read more: All that slipping and sliding on tennis courts prevents injuries: a biomechanics expert explains how
For the men it’s less so clear. So in response to the question of who is the best male tennis player of the modern era, the answer is “it depends”.

If pressed for an answer, it’s hard to go past Rafael Nadal. He has dominated a grand slam (French Open) unlike the other players, while remaining competitive in the other three slams.
A more comprehensive analysis would consider data from all tournaments, not just grand slams, and this would help to reduce uncertainty in the winning probability estimates.
It should also be noted that these are retrospective winning probability estimates, and cannot be used to predict outcomes for future tournaments. Predictive statistical models would focus on more recent tennis data.

