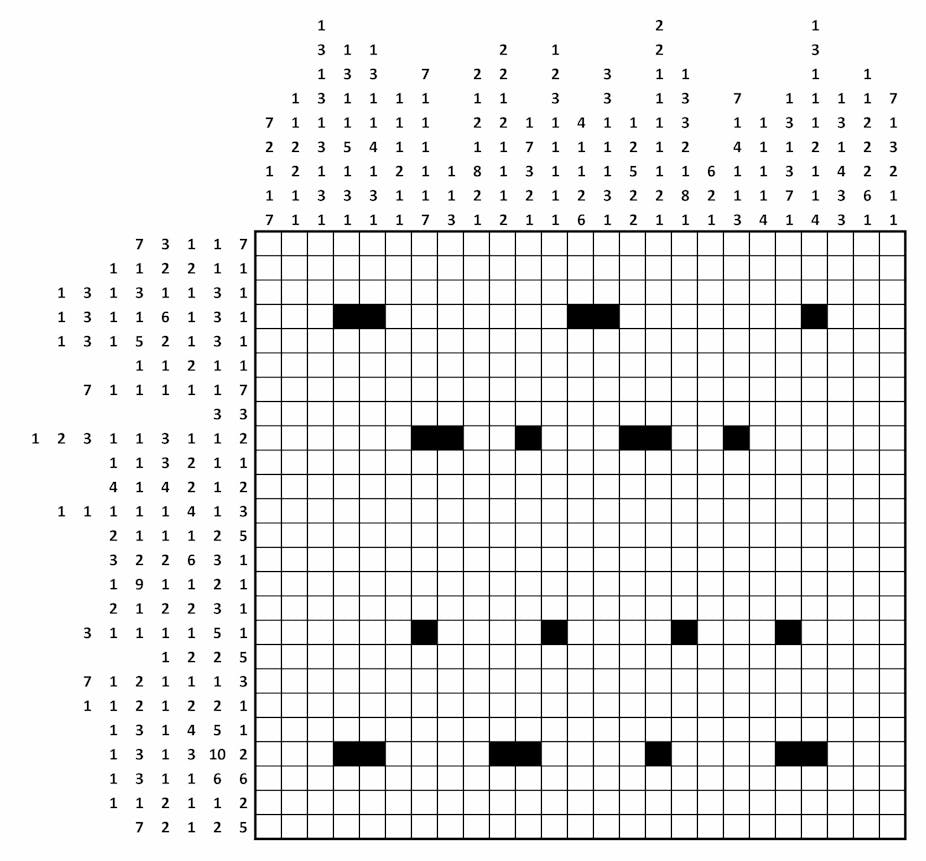
Calling all aspiring spooks. Robert Hannigan, director of Britain’s security and intelligence organisation GCHQ, has included a rather tantalising puzzle with his Christmas card this year. He hopes that it will exercise your grey cells over the holiday period.
If you can solve the puzzle, along with the others that it will lead to, you can email the solution to GCHQ (the Government communications headquarters) before January 31. A winner will be drawn from all the correct answers – and doubtless be named to much fanfare.
So what do you need to do to be in with a chance?
The puzzle requires that you shade in squares on the 25x25 grid shown above. But which ones? Well, a few of the “black” squares have been completed for you, but most you will have to do yourself. By way of a clue, each row and cell has a sequence of numbers attached to it. The numbers represent a sequence of shaded cells, that need to separated from each other by at least one blank cell. For example, the row marked “7 3 1 1 7” should contain a sequence of seven shaded cells, followed by at least one blank cell, then three shaded cells, followed by at least one blank cell – and so on. The problem is made trickier because each horizontal row intersects a vertical column, each with its own sequence code.
Paper and pen
So how do you reach the solution? One way of cracking it is to resort to old-fashioned paper and pen. Just sit down, put on your thinking cap and try to reason it out.
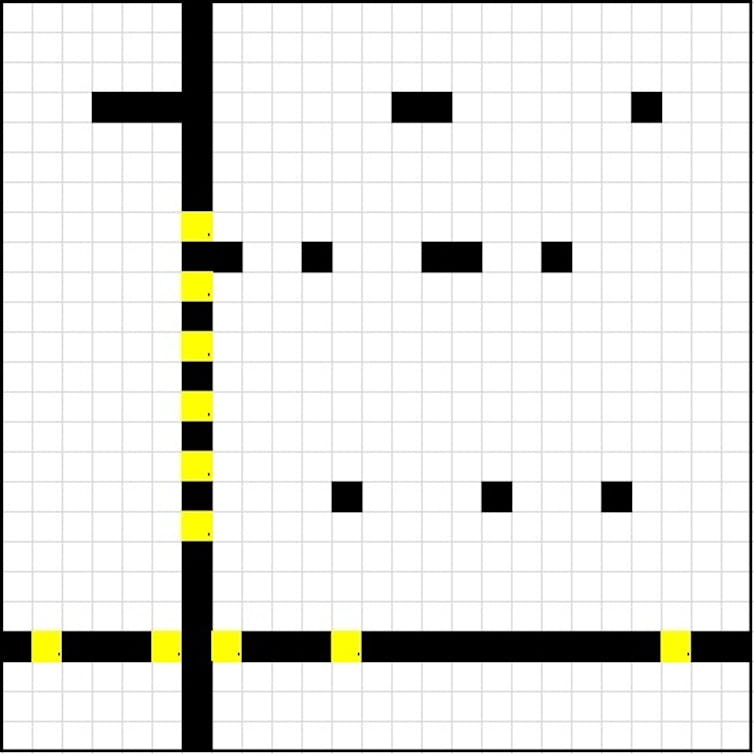
It is not that difficult to get started. In fact, it is already started, and it is easy to fill in a few more squares. Take a look at row 22 on the horizontal axis – the one that has the sequence “1 3 1 3 10 2”. These numbers add up to 20 and as there are six blocks, you need at least five blank squares to separate them. As we only have 25 squares in the row, this pattern can only fit in one way – the first square in the row has to be shaded, and the rest just follow, with only one blank square between each run of shaded squares.
Are there any others like this? Column seven (“7 1 1 1 1 1 7”) sums up to 19. As we have seven numbers we need at six least separators. This also adds up to 25, so this row is easy to complete, too. The figure below shows the grid once we have filled in row 22 and column seven (the blank squares are marked in yellow).
Any others where the row or column is also easy to complete? Yes, but I’ll leave it to you to find them.
Once you have completed the “easy” rows/columns, you then need to start looking for other ways of completing the remaining rows and columns, or even reasoning about individual cells. In many ways, it is like completing a Sudoku puzzle. You should find that you never have to guess, but perhaps using a pencil and having a rubber to hand might be a good idea.
One more hint, colour in the blank squares, too – just use a different shade. This might sound obvious but leaving a square blank, once you have determined that it “must” be blank, might mean that it gets mistakenly shaded later. You can see in the figure above that I’ve have coloured the blank squares yellow, so we know that we should not make them black later.
Getting mathematical
If you don’t want to exercise the brain, you can get a computer to do it for you.
Jean Francois Puget presents one such – SPOILER ALERT: the next link reveals the solution – methodology, which is based on mixed integer programming.
You define the problem using variables, zeroes for white cells and ones for black cells. You next define constraints. For example, each row/column has to have the correct sequence of blacks cells in each row/column, separated by at least one white cell. You also need to define an objective function. This is usually something you are trying to minimise (for example, waste) or maximise (for example, profit). In the case of this puzzle, there is nothing to minimise or maximise, as once we have a valid solution we cannot improve on it.
Once we have defined the variables, constraints and objection function, we can hand it over to one of the many solvers that are available online and it will return the solution.
The downside of mathematical approaches to complex problems is that there may be a solution, but it could take millions of years to find it. Fortunately, this puzzle can be solved quickly.
Other approaches
If you don’t fancy either of the above two approaches, there are many other options. In a previous article we discussed how ants could be used to solve chess puzzles. So if ants can play chess, they could certainly solve the GCHQ puzzle.
Whether it is worth the effort to develop the computer model required, however, is open to debate. The same could also be argued for the many other meta-heuristic approaches. Almost any of them could solve this puzzle, but is it worth the development effort?
The puzzle has generated a lot of media interest and many people are trying to solve it. As we have shown above, there are already solutions on the internet and there is even more information about the subsequent puzzles on Reddit. That does seem to go against the spirit of the puzzle, however, and the spirit of the season. Why not just print the grid, get out a pen and exercise the grey matter sometime over the festive period? You may even win the honest way.