MILLENNIUM PRIZE SERIES: The Millennium Prize Problems are seven mathematics problems laid out by the Clay Mathematics Institute in 2000. They’re not easy – a correct solution to any one results in a US$1,000,000 prize being awarded by the institute.
Russian mathematician Grigori Perelman was awarded the Prize on March 18 last year for solving one of the problems, the Poincaré conjecture – as yet the only problem that’s been solved. Famously, he turned down the $1,000,000 Millennium Prize.
Over the coming weeks, each of these problems will be illuminated by experts from the Australian Mathematical Sciences Institute (AMSI) member institutions.
Here, Daniel Delbourgo explains the Birch and Swinnerton-Dyer Conjecture. Enjoy.
Elliptic curves have a long and distinguished history that can be traced back to antiquity. They are prevalent in many branches of modern mathematics, foremost of which is number theory.
In simplest terms, one can describe these curves by using a cubic equation of the form
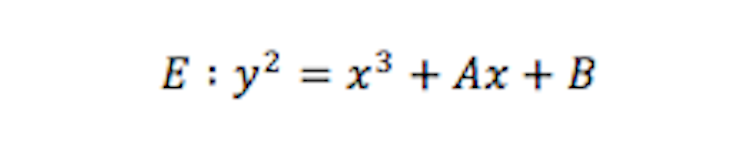
where A and B are fixed rational numbers (to ensure the curve E is nice and smooth everywhere, one also needs to assume that its discriminant 4A3 + 27B2 is non-zero).
To illustrate, let’s consider an example: choosing A=-1 and B=0, we obtain the following picture:
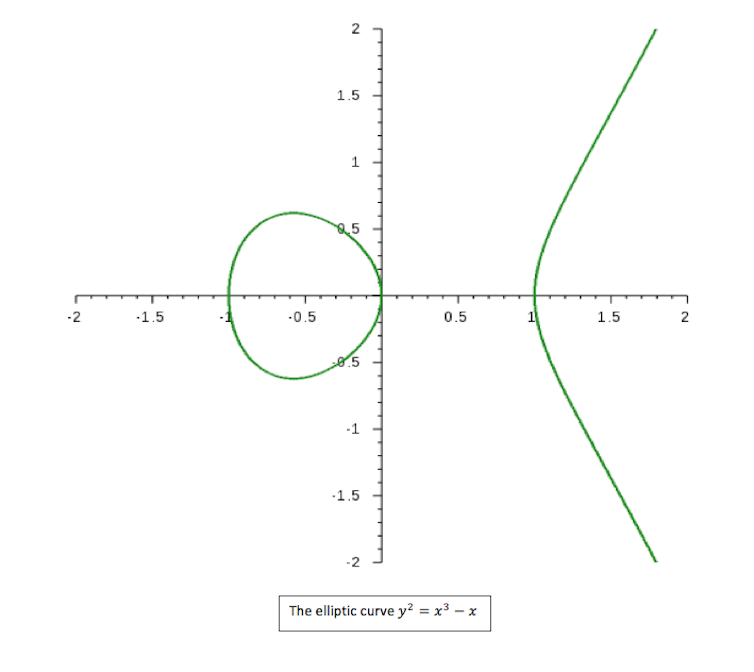
At this point it becomes clear that, despite their name, elliptic curves have nothing whatsoever to do with ellipses! The reason for this historical confusion is that these curves have a strong connection to elliptic integrals, which arise when describing the motion of planetary bodies in space.
The ancient Greek mathematician Diophantus is considered by many to be the father of algebra. His major mathematical work was written up in the tome Arithmetica which was essentially a school textbook for geniuses. Within it, he outlined many tools for studying solutions to polynomial equations with several variables, termed Diophantine Equations in his honour.
One of the main problems Diophantus considered was to find all solutions to a particular polynomial equation that lie in the field of rational numbers Q. For equations of “degree two” (circles, ellipses, parabolas, hyperbolas) we now have a complete answer to this problem. This answer is thanks to the late German mathematician Helmut Hasse, and allows one to find all such points, should they exist at all.
Returning to our elliptic curve E, the analogous problem is to find all the rational solutions (x,y) which satisfy the equation defining E. If we call this set of points E(Q), then we are asking if there exists an algorithm that allows us to obtain all points (x,y) belonging to E(Q).
At this juncture we need to introduce a group law on E, which gives an eccentric way of fusing together two points (p₁ and p₂) on the curve, to obtain a brand new point (p₄). This mimics the addition law for numbers we learn from childhood (i.e. the sum or difference of any two numbers is still a number). There’s an illustration of this rule below:
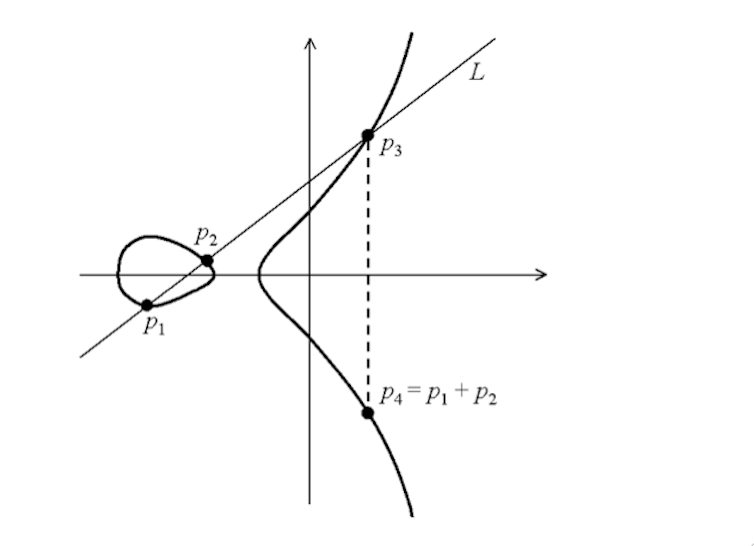
Under this geometric model, the point p₄ is defined to be the sum of p₁ and p₂ (it’s easy to see that the addition law does not depend on the order of the points p₁, p₂). Moreover the set of rational points is preserved by this notion of addition; in other words, the sum of two rational points is again a rational point.
Louis Mordell, who was Sadleirian Professor of Pure Mathematics at Cambridge University from 1945 to 1953, was the first to determine the structure of this group of rational points. In 1922 he proved

where the number of copies of the integers Z above is called the “rank r(E) of the elliptic curve E”. The finite group ΤE(Q) on the end is uninteresting, as it never has more than 16 elements.


