MILLENNIUM PRIZE SERIES: The Millennium Prize Problems are seven mathematics problems laid out by the Clay Mathematics Institute in 2000. They’re not easy – a correct solution to any one results in a US$1,000,000 prize being awarded by the institute.
Russian mathematician Grigori “Grisha” Perelman was awarded the Prize on March 18 last year for solving one of the problems, the Poincaré conjecture – as yet the only one that’s been solved. Famously, he turned down the $1,000,000 Millennium Prize.
Over the coming weeks, each of these problems will be illuminated by experts from the Australian Mathematical Sciences Institute (AMSI) member institutions.
Here, Hyam Rubinstein discusses the now-resolved Poincaré Conjecture. Enjoy.
In 1904, French mathematician Henri Poincaré asked a key question about three-dimensional spaces (“manifolds”).
Imagine a piece of rope, so that firstly a knot is tied in the rope and then the ends are glued together. This is what mathematicians call a knot. A link is a collection of knots that are tangled together.
It has been observed that DNA, which is coiled up within cells, occurs in closed knotted form.
Complex molecules such as polymers are tangled in knotted forms. There are deep connections between knot theory and ideas in mathematical physics. The outsides of a knot or link in space give important examples of three-dimensional spaces.
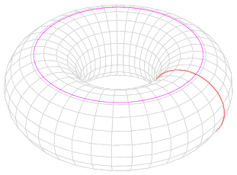
Back to Poincaré and his conjecture. He asked if the 3-sphere (which can be formed by either adding a point at infinity to ordinary three-dimensional Euclidean space or by gluing two solid three-dimensional balls together along their boundary 2-spheres) was the only three-dimensional space in which every loop can be continuously shrunk to a point.
Poincaré had introduced important ideas in the structure and classification of surfaces and their higher dimensional analogues (“manifolds”), arising from his work on dynamical systems.
Donuts to go, please
A good way to visualise Poincaré’s conjecture is to examine the boundary of a ball (a two-dimensional sphere) and the boundary of a donut (called a torus). Any loop of string on a 2-sphere can be shrunk to a point while keeping it on the sphere, whereas if a loop goes around the hole in the donut, it cannot be shrunk without leaving the surface of the donut.
Many attempts were made on the Poincaré conjecture, until in 2003 a wonderful solution was announced by a young Russian mathematician, Grigori “Grisha” Perelman.
This is a brief account of the ideas used by Perelman, which built on work of two other outstanding mathematicians, Bill Thurston and Richard Hamilton.
3D spaces
Thurston made enormous strides in our understanding of three-dimensional spaces in the late 1970s. In particular, he realised that essentially all the work that had been done since Poincaré fitted into a single theme.
He observed that known three-dimensional spaces could be divided into pieces in a natural way, so that each piece had a uniform geometry, similar to the flat plane and the round sphere. (To see this geometry on a torus, one must embed it into four-dimensional space!).
Thurston made a bold “geometrisation conjecture” that this should be true for all three-dimensional spaces. He had many brilliant students who further developed his theories, not least by producing powerful computer programs that could test any given space to try to find its geometric structure.
Thurston made spectacular progress on the geometrisation conjecture, which includes the Poincaré conjecture as a special case. The geometrisation conjecture predicts that any three-dimensional space in which every loop shrinks to a point should have a round metric – it would be a 3-sphere and Poincaré’s conjecture would follow.
In 1982, Richard Hamilton published a beautiful paper introducing a new technique in geometric analysis which he called Ricci flow. Hamilton had been looking for analogues of a flow of functions, so that the energy of the function decreases until it reaches a minimum. This type of flow is closely related to the way heat spreads in a material.
Hamilton reasoned that there should be a similar flow for the geometric shape of a space, rather than a function between spaces. He used the Ricci tensor, a key feature of Einstein’s field equations for general relativity, as the driving force for his flow.
He showed that, for three-dimensional spaces where the Ricci curvature is positive, the flow gradually changes the shape until the metric satisfies Thurston’s geometrisation conjecture.
Hamilton attracted many outstanding young mathematicians to work in this area. Ricci flow and other similar flows have become a huge area of research with applications in areas such as moving interfaces, fluid mechanics and computer graphics.
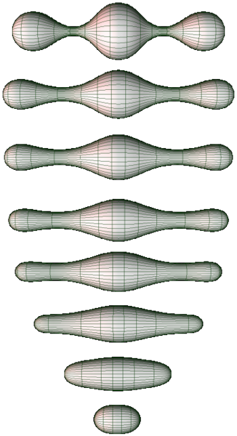
He outlined a marvellous program to use Ricci flow to attack Thurston’s geometrisation conjecture. The idea was to keep evolving the shape of a space under Ricci flow.
Hamilton and his collaborators found the space might form a singularity, where a narrow neck became thinner and thinner until the space splits into two smaller spaces.
Hamilton worked hard to try to fully understand this phenomenon and to allow the pieces to keep evolving under Ricci flow until the geometric structure predicted by Thurston could be found.
Perelman
This is when Perelman burst on to the scene. He had produced some brilliant results at a very young age and was a researcher at the famous Steklov Institute in St Petersburg. Perelman got a Miller fellowship to visit UC Berkeley for three years in the early 1990s.
I met him there around 1992. He then “disappeared” from the mathematical scene for nearly ten years and re-emerged to announce that he had completed Hamilton’s Ricci flow program, in a series of papers he posted on the electronic repository called ArXiv.
His papers created enormous excitement and within several months a number of groups had started to work through Perelman’s strategy.
Eventually everyone was convinced that Perelman had indeed succeeded and both the geometrisation and Poincaré conjecture had been solved.
Perelman was awarded both a Fields medal (the mathematical equivalent of a Nobel prize) and also offered a million dollars for solving one of the Millenium prizes from the Clay Institute.
He turned down both these awards, preferring to live a quiet life in St Petersburg. Mathematicians are still finding new ways to use the solution to the geometrisation conjecture, which is one of the outstanding mathematical results of this era.
This is the fourth part of the Millennium Prize Series. To read the other instalments, follow the links below.

