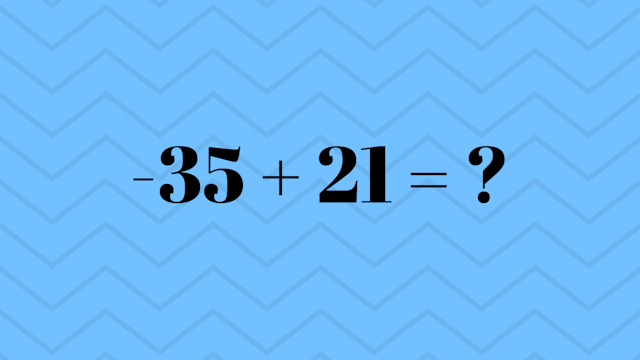Pembelajaran matematika di sekolah dasar didesain untuk mendorong para siswa berpikir sistematis, kritis, analitis, logis, dan kreatif sesuai dengan kemampuan anak.
Matematika juga berfungsi untuk mengembangkan kemampuan komunikasi dengan menggunakan bilangan dan simbol untuk menyelesaikan persoalan matematis. Di sekolah dasar, kurikulum matematika menekankan aspek bilangan, geometri dan pengukuran, dan pengolahan data.
Masalahnya, dalam proses pembelajaran operasi dasar aritmatika (penjumlahan, pengurangan, perkalian dan pembagian) kerap kali guru “menyembunyikan” tanda dan proses berhitung yang semestinya disampaikan secara transparan kepada para siswa. Kadang-kadang guru dan buku rujukan lebih fokus pada orientasi hasil ketimbang proses penyelesaikan soal yang logis benar dan transparan.
Selama berabad-abad, guru mengajarkan metode vertikal–metode berhitung yang prosesnya dapat dilakukan secara terstruktur dari atas menuju bawah–untuk menyelesaikan soal aritmatika. Dalam beberapa tahun terakhir, saya mengembangkan dan menguji-cobakan metode horizontal (metris), yakni metode perhitungan yang proses penyelesaian dilakukan secara mendatar (horizontal). Metode ini bisa dipakai sebagai metode alternatif untuk pengajaran penyelesaian soal.
Saya dan kolega melakukan riset dengan melatih penggunaan metode horizontal untuk operasi penjumlahan, pengurangan, dan perkalian kepada 37 guru sekolah dasar di Cisauk, Tangerang, pada 2015. Dari jumlah itu 34 di antaranya menerapkan metode ini di kelas setelah pelatihan. Enam bulan kemudian hasil pengajaran metode ini dites melalui kompetisi aritmatika antarsiswa sekolah dasar di kecamatan tersebut yang menerapkan metode ini. Hasilnya, pembelajaran metris meningkatkan kemampuan para siswa dalam menjawab soal dengan lebih cepat dan lebih baik.
Sebuah riset lainnya juga menunjukkan penggunaan metode horizontal dapat meningkatkan kemampuan berhitung dalam konsep pembagian pada anak tuna rungu di sekolah dasar Nagreg Bandung.
Pembelajaran aritmetika dapat berkualitas apabila proses berhitung yang menggunakan simbol matematis dapat dilakukan secara logis benar dan transparan.
Logis benar artinya setiap langkah dalam proses berhitung harus selalu berdasarkan aturan yang telah ditetapkan oleh definisi pada simbol matematis tersebut.
Sedangkan transparan berarti setiap langkah dalam proses berhitung yang benar tersebut sampai diperoleh hasil akhirnya dapat diperlihatkan secara terbuka.
Dalam proses hitungnya sejak awal hingga hasil akhirnya harus selalu dihubungkan dengan tanda sama-dengan (=).
Masalah metode berhitung

Suatu hari saya menerima kiriman foto halaman buku matematika dari seorang ibu yang anaknya masih belajar di sekolah dasar kelas 2. Foto tersebut memuat proses pembelajaran penjumlahan dengan bilangan negatif atau pengurangan dengan metode vertikal.
Proses pembelajaran pengurangan tersebut menjelaskan suatu persoalan apabila harga mutlak pada bilangan negatif lebih besar dari pada bilangan positifnya, seperti soal -35 + 21 = 21 – 35. Proses penyelesaiannya dengan metode vertikal sebagai berikut:
- Langkah pertama, abaikan tanda negatif.
- Langkah kedua, kurangi bilangan terbesar (35) dengan bilangan terkecil (21), 35 – 21 = 14.
- Langkah ketiga, beri tanda pada bilangan hasilnya sesuai dengan tanda pada bilangan terbesar (21 – 35 = -14).
Metode berhitung ini termasuk logis benar karena bila langkah tersebut diterapkan maka hasil akhirnya tidak salah.
Tapi apakah cara berhitung di atas termasuk logis benar dan transparan? Ternyata jawabnya tidak, karena setiap langkah hitungnya yang dimulai dari soal awal hingga hasil akhirnya tidak selalu dihubungkan dengan tanda sama dengan (=).
Saya kemudian bertanya ke guru matematika SD dan jawabannya mengejutkan. Dia menjelaskan bahwa sebagian proses berhitungnya tidak perlu diperlihatkan langkah per langkahnya alias disembunyikan, lalu hasil akhirnya saja yang ditulis pada lembar jawaban.
Bila proses pembelajaran seperti ini yang dikembangkan, guru telah gagal mengajarkan kepada para siswa untuk tetap berpikir logis benar dan transparan.
Metode vertikal vs horizontal
Lalu bagaimana agar proses pendidikan berhitung tersebut dapat logis benar dan transparan? Solusinya ada dua cara. Pertama soal itu dapat diselesaikan tetap menggunakan metode konvensional/vertikal tapi bukan seperti yang terdapat pada buku panduan tersebut. Atau, kedua, dengan memanfaatkan metode horizontal.
Pertama, bila menggunakan metode konvensional maka konsep sifat perkalian antara tanda negatif dan negatif menjadi positif harus sudah diketahui oleh siswa SD.
Pemenuhan syarat ini bisa jadi merupakan kekurangan dari cara konvensional karena konsep perkalian antar bilangan negatif belum diberikan kepada siswa SD di tingkat awal seperti siswa kelas 1 atau 2. Proses penjelasan cara berhitung 21 – 35 agar dapat tetap logis benar dan transparan adalah 21 – 35 = - (- 21 + 35) = - (35 – 21) = - 14.
Sedangkan untuk memperoleh hasil pengurangan 35 – 21 prosesnya dapat menggunakan metode konvensional secara logis benar dan transparan yang biasa sudah diajarkan oleh para guru SD.
Kedua, bila penyelesaiaan soal 21 – 35 menggunakan bantuan metode horizontal maka persyaratan pemahaman siswa akan konsep perkalian antar bilangan negatif yang mesti dipenuhi oleh metode konvensional di atas tidak dibutuhkan lagi. Sehingga proses pembelajaran pengurangan yang logis benar dan transparan dapat lebih awal diberikan ke para siswa SD dengan memanfaatkan metode ini.
Dalam metris terdapat notasi pagar (|) yang berfungsi sebagai pengelompokan nilai tempat bilangan satuan, puluhan, ratusan, dan ribuan. Proses penjumlahan atau pengurangan dapat dilakukan oleh bilangan yang mempunyai nilai tempat yang sama.
Notasi pagar tersebut dapat dilepas apabila jumlah pagar sama dengan jumlah angka di sebelah kanannya dan tanda positif (negatif) pada setiap angka diantara semua notasi pagar harus sama.
Dengan bantuan metode horizontal dapat dibuktikan bahwa proses perhitungan 21 – 34 dapat tetap benar dan transparan yaitu (2|1) – (3|5) = 2-3|1-5 = -1|-4 = - (1|4) = - 14.
Sedangkan untuk penjelasan 2-3 = -1 atau 1-5 = -4 dapat diterangkan dengan mudah menggunakan garis bilangan. Hal ini dapat terjadi karena dengan bantuan metode horizontal maka soal penjumlahan dan pengurangan dengan bilangan puluhan, ratusan, dan ribuan dapat dicacah menjadi bilangan paling kecil yaitu berupa bilangan satuan sehingga dengan mudah mampu divisualisasikan oleh siswa-siswi sekolah dasar.
Kurikulum pendidikan matematika dasar dengan proses pengajaran yang selalu dijaga agar tetap logis benar dan transparan dalam memecahkan masalah aritmetika sangat penting. Model kurikulum pembelajaran seperti ini akan membuat para siswa SD dapat lebih baik memahami proses berhitung.
Dengan metode berhitung yang logis benar dan transparan, pemahaman siswa diharapkan dapat meningkat dan menjadi dasar untuk pengembangan kemampuan siswa bidang matematika tingkat pendidikan berikutnya. Kementerian Pendidikan dan Kebudayaan seharusnya menerima inovasi metode belajar yang logis benar dan transparan agar kualitas pendidikan Indonesia makin menanjak.