Recently, as a community ambassador for ANU Student Equity, I took to a local secondary school to talk maths with a small group of students.
The goal? To give them an enjoyable mathematical experience and a glimpse at what maths is all about.
I started by asking them what they thought about maths. The response was that they didn’t much care for sums - a calculator was more likely to pursue such a career.
I knew I had to snap this misconception that “maths” was another way to say “dull arithmetic” and I had to do it fast - iPhones were starting to appear under the desks.
A colouring exercise
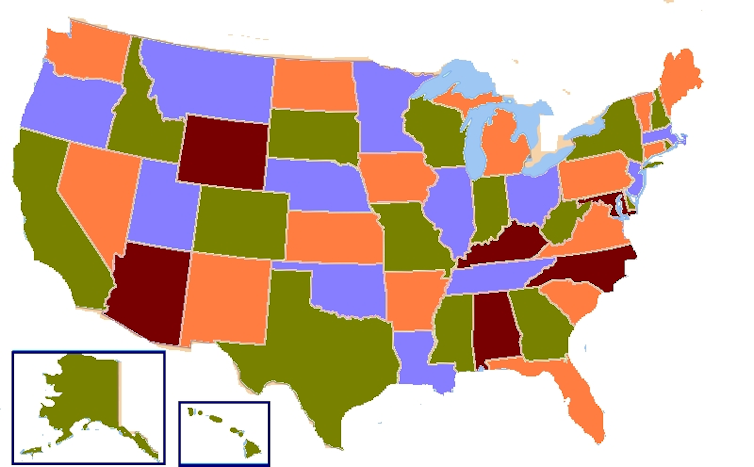
“Draw a map of Australia,” I told them. “Outline the states, and then colour the states in. Oh, but don’t let any two adjacent states be the same colour - it wouldn’t look very nice.”
They coloured happily, naively thinking themselves free of having to do any maths.
After walking around the classroom admiring their handiwork, I asked them the following question:
What is the least number of colours needed to colour in Australia this way?
They were pretty quick here, even though some had gone mad with the visible spectrum whereas others had been a bit more conservative. After a short amount of time, the class agreed on the answer as three:

I congratulated them on their work before giving them the following two exercises.
1. Invent a country (with states) where the minimal number of colours needed is four. Swap with a classmate and get them to colour it in.
2. Invent another country where the minimal number of colours needed is five. Swap your map with a classmate and get them to colour it in.
Well, the students had a blast creating and naming their own countries. They challenged their friends in the first exercise, as the way to colour was not always obvious.
The following is the simplest example of a map that requires four colours:
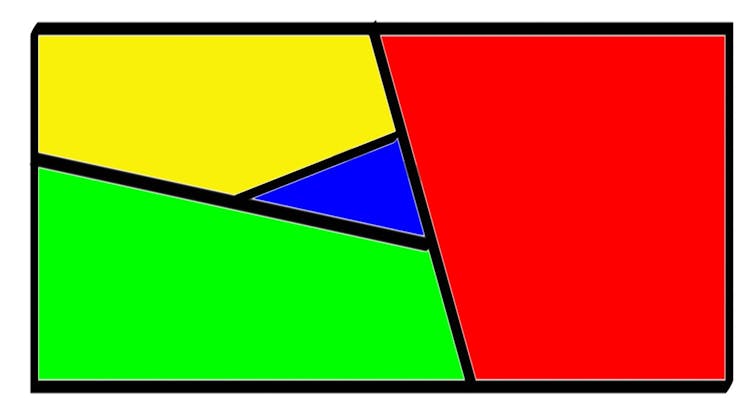
The second exercise went exactly as I had hoped. There was some conflict: it turned out that even though the minimal number of colours was intended to be five, students were colouring in the maps correctly using only four.
One by one, we drew up each student’s map on the board and took turns showing that, in fact, each of them could be filled correctly using only four colours. Madness! I let them have another failed attempt, before letting them in on a well known mathematical theorem.
The four colour theorem
You never need more than four colours to colour in the regions of a map, such that any two adjacent regions are differently coloured.
We also have to stipulate that adjacent regions are those that share an edge, so regions that meet at a point are not deemed to be adjacent.
“This is probably the first example of real mathematics you’ve ever seen,” I told them. “Maths is about ideas, not arithmetic.” They wanted to know a bit more about it.
We talked about how, in 1852, a mathematician called Francis Guthrie was colouring in the different counties of England, and noticed that only four colours were needed. He wrote this in a letter to his brother Frederick, who passed it on to another mathematician.
For over a century, different mathematicians would fail in their attempts to prove the four colour theorem. But in 1976, Kenneth Appel and Wolfgang Haken finally succeeded.
Upon asking the students how one might prove this mighty theorem, there was a suggestion we could draw every possible map and then colour them in using only four colours.
I shut them down quickly with the following fact: there are infinitely possible maps. So how did they prove it?
The idea behind the proof
The four colour theorem serves as the first major mathematical theorem to be proved using a computer. Of course, there are some stunning ideas behind the computation.
To show that there are no maps that need more than four colours, Appel and Haken turned to reductio ad absurdum (reduction to absurdity), the greatest weapon the mathematician has. Here’s how it works:
If we want to prove that something is true, we instead assume that it is false and show that the rest of maths goes bad. That is, by assuming falsity, we encounter contradictions to already known truths.

This tells us that our original assumption is incorrect, and that what we want to prove must be true.
Appel and Haken used this idea as follows. They assumed to the contrary, that there was some map out there which required more than four colours. They then showed that this rogue map was not allowed to contain within it one of 1,936 special, smaller maps.
Appel and Haken then showed that any map has to contain one of these special smaller maps and so appeared the contradiction.
There was a lot of checking to be done in the proof, so Appel and Haken wrote a computer program to do most of the working. As such, the four colour theorem was the first major mathematical theorem to be proved using a computer.
The doubts
The computer plays the biggest role in the proof and so there were concerns about the truth of this theorem, as it’s essentially impossible to verify by hand. As such, there were many sceptics.
In 1975, as an April Fool’s joke, the American mathematics writer Martin Gardner spread around a proposed counterexample to the four colour theorem. It took 24 years (and a lot of computer time) to show that only four colours were needed.
Even today, despite enjoying widespread academic acceptance, there are still sceptics who doubt the four colour theorem.
Can you come up with a counter-example?

