The Crystal Maze, the popular UK television show from the early 1990s, included a puzzle that is very useful for explaining one of the main conundrums in artificial intelligence. The puzzle appeared a few times in the show’s Futuristic Zone, one of four zones in which a team of six contestants sought to win “time crystals” that bought time to win prizes at the Crystal Dome at the end of the show.
Never solved in the two-minute time frame, the puzzle was based on a network of connected red circles (see clip below). On the wall was written a clue: “No consecutive letters in adjacent circles”. The letters A to H were printed on circular plates which could be fitted onto each circle.
So what is the right approach? We might start by considering which circles are hardest to label. With a little thought, you might choose the two middle circles, since they have the most connections. Now consider which letters might best be put on them: A and H are natural candidates because they each have only one neighbour (B and G, respectively). We might put them into the grid like this:
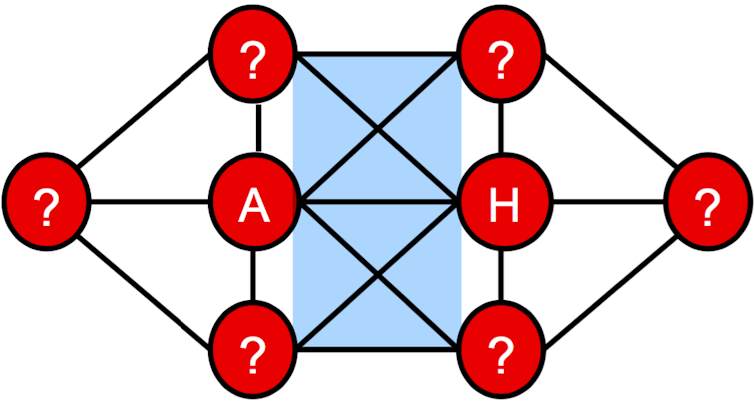
We can now do some deduction to eliminate incompatible possibilities for the other circles. For example the top-left circle is connected to both of the central circles. Since no consecutive letters can appear in connected circles, it can’t now contain B or G. Similar reasoning can be applied to the top-right, bottom-left, and bottom-right circles:
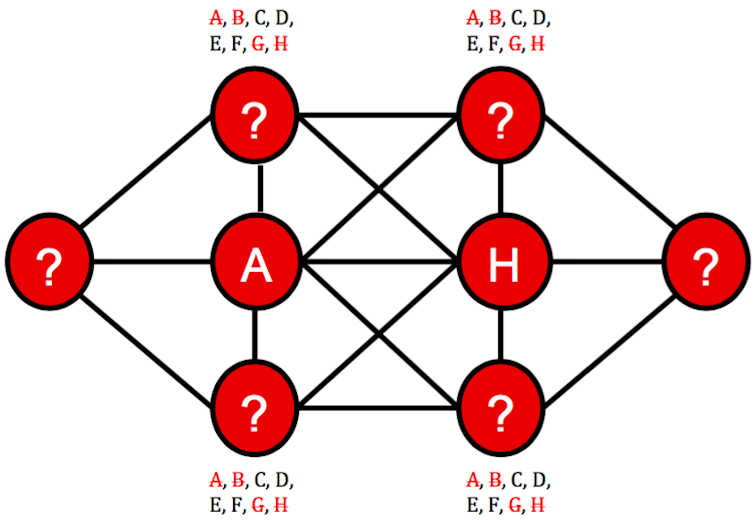
The leftmost and rightmost circles have to be treated differently, since each is only adjacent to one central circle. On the left we can rule out B, and on the right we can rule out G:
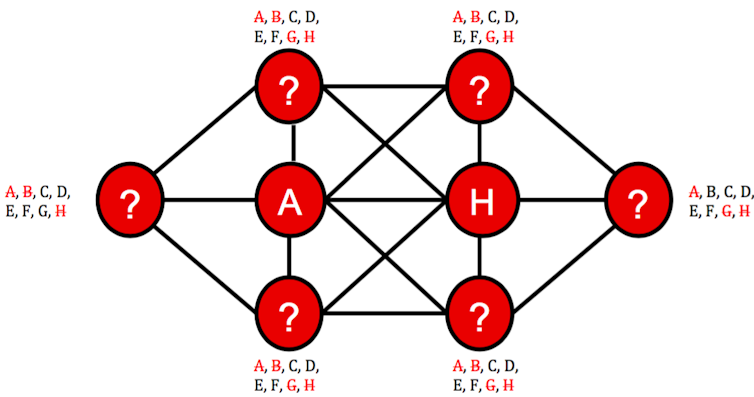
Look carefully at the remaining options and only the leftmost circle still has G as a possibility, and only the rightmost circle has B. Once we put them in place, we can remove further possibilities from the adjacent circles:
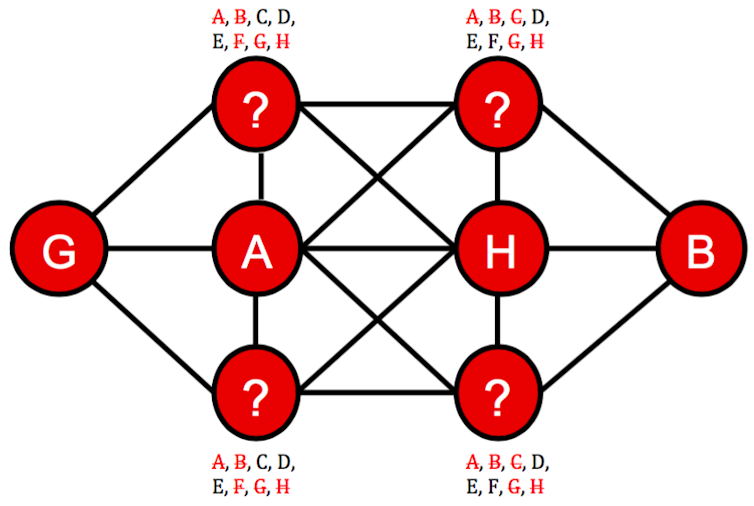
It is now time to make another guess. It seems reasonable to start with the top-left circle and try its first possibility: C. This allows us to rule out D from the adjacent circle and C from the bottom left. If we now guess E for the top-right circle, the bottom-left circle has only one possibility left, D, which leaves just F for the bottom-right circle. We have a solution:
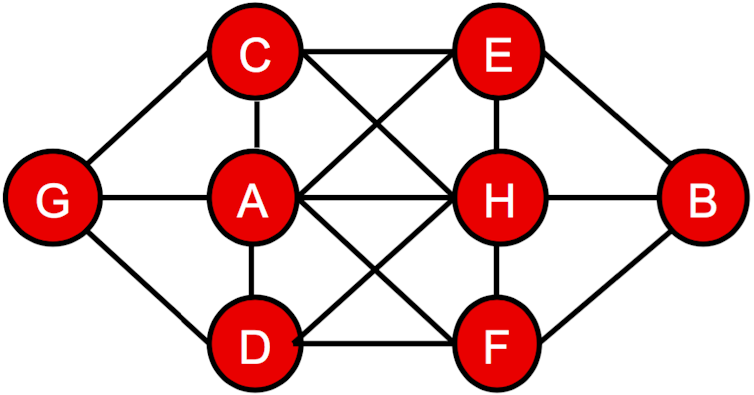
Decisions, decisions
This puzzle is an example of a much wider class of decision-making problems that arise in our lives, such as rostering decisions in a hospital or factory, scheduling buses or trains, or designing medical experiments. To save us the aggravation of coming up with the best solutions, one of the challenges for artificial intelligence is to develop a general way of representing and reasoning about them.
One method is known as the constraint satisfaction problem. Just like our Crystal Maze puzzle, problems that fit this model involve a set of required decisions (“cover each circle with a plate”); a fixed set of possibilities (“use the plates from A to H provided”); and a set of constraints that allow only certain combinations of possibilities (“no consecutive letters in adjacent circles”). If you input the requirements for your particular problem into a piece of software known as a constraint solver, it can then try to solve it. It will do this in much the same way as we solved the puzzle: it combines guessing (we call this “search”) with deduction, ruling out possibilities that cannot be part of a solution based on the decisions made so far.
The greatest challenge for programmers in this field is that as you increase the size of the input problem, it quickly becomes much harder to find solutions. This is directly related to how the software “guesses” the answer. Although our guesses proved correct in our simple puzzle, in AI they can often lead us down blind alleys. With large problems there can be a vast number of possibilities and a similarly vast number of dead ends.
One key question is whether there is some way of reaching solutions without going down these alleys. As yet, we don’t know. This directly relates to one of the most important open questions in computer science, the P vs NP problem, for which the Clay Mathematics Institute in the US is offering Us$1m (£657,000) for a solution. It essentially asks whether every problem whose answer can be checked quickly by a computer can also be quickly solved by a computer.
Until someone solves it, the prevailing view is that it cannot. If so, our software does have to search through all the possible guesses, in which case we need to make it as efficient as possible. One important factor here is the search strategy – which decision we tell the computer to focus on next and which value we assign to it. Also very important is what we decide are the requirements for the particular problem. Mapping our puzzle to a constraint satisfaction template was straightforward, but in real life there are often many different options. Choosing the right strategy and model can be the difference between finding a quick solution and failing in any practical amount of time.
We have now reached the stage where the latest constraint-solving software can solve far more complex practical problems than, say, ten years ago. It was used to plan the scientific activities of the Philae comet lander last year, for instance. It also offers a better way of organising evacuation schedules for large-scale disasters.

Constraint solving has found most success with scheduling problems, but there are other similar AI tools that are more useful for other types of questions. We won’t go into them here, but they include the likes of propositional satisfiability, evolutionary algorithms and mathematical programming techniques. The job of specialists is to analyse a problem, identify which combination of tools will be the most successful for a particular case, and put together a bespoke piece of software. Once computers can do this analysis and identification, hopefully only a few years in the future, we will have made a huge leap forward. Meanwhile, the battle to make each of these tools as powerful as possible continues.

