In math class, you probably learned how to compute the area of lots of different shapes by memorizing algebraic formulas. Remember “base x height” for rectangles and “½ base x height” for triangles? Or “𝜋 x radius²” for circles?
But if you were in math class in ancient Greece, you might have learned something very different. Ancient Greek mathematicians, such as Euclid, thought of area as something geometric, not algebraic. Euclid’s geometric perspective, recorded in his foundational work “Elements,” has influenced research programs across centuries – even the work of mathematicians today, like the two of us.

Modern mathematicians refer to Euclid’s concept of “having equal area” as “being scissors congruent.” This idea, based on cutting up shapes and pasting them back together in different ways, has inspired interesting mathematics beyond just computing areas of triangles and squares. The story of scissors congruence demonstrates how classical problems in geometry can find new life in the strange world of abstract modern math.
Euclid’s notion of area
Today, people think of the area of a shape as a single number that can be computed using algebraic formulas or calculus. So what does it mean to think of area as something geometric the way the ancient Greeks did?
Imagine you’re back in math class and you have a pair of scissors, some tape and a piece of construction paper. Your teacher instructs you to make a new flat, two-dimensional shape using all of the construction paper and only straight-line cuts. Using your scissors, you cut the paper into a bunch of pieces. You start moving these pieces around – maybe you rotate them or flip them over – and you tape them back together to form a new shape.

Using your algebraic formulas for area, you could check that the area of your new shape is equal to the original area of the construction paper. No matter how a 2D shape is cut up – as long as all the pieces are taped back together without overlap – the area of the old and the new shape will always be equal.

For Euclid, area is the measurement that is preserved by this geometric “cutting-and-pasting.” He would say that the new shape you made is “equal” to the original piece of construction paper – mathematicians today would say the two are “scissors congruent.”
What can your new shape look like? Because you’re only allowed to make straight-line cuts, it has to be a polygon, meaning none of the sides can be curved.

Could you have made any possible polygon with the same area as your original piece of paper? The answer, amazingly, is yes – there’s even a step-by-step guide from the 1800s that tells you exactly how to do it.
In other words, for polygons, Euclid’s notion of area is exactly the same as the modern one. In fact, you may have even used Euclid’s idea of area before in computations without knowing it.
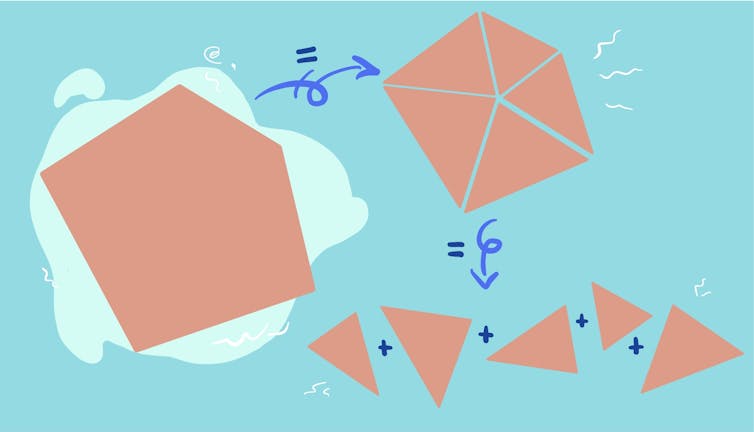
For example, you can use scissors congruence to compute the area of a pentagon. Since area is preserved if you cut the pentagon up into smaller triangles, you can instead find the area of these triangles (using “½ base x height”) and add them up to get the answer.
Hilbert’s third problem
Perhaps the most infamous appearance of scissors congruence is on the famous German mathematician David Hilbert’s list of problems, which consisted of some of the most important mathematical questions of the 1900s. Of the original 23 problems Hilbert proposed, some have been solved, some have been shown to be unsolvable and others are still unresolved. The third problem on the list, and the first to be resolved, is about scissors congruence.
Instead of two-dimensional polygons, Hilbert asked about their three-dimensional cousins: polyhedra. Euclid’s notion of scissors congruence was known to be an accurate description of two-dimensional area, but could it be a good notion of three-dimensional volume?

The answer came within a year, provided by one of Hilbert’s students, Max Dehn. Dehn’s solution to the problem was very different from the two-dimensional case. He showed that when polyhedra are cut up, volume is not the only thing that is preserved. There is another preserved measurement, now called the Dehn invariant, which is constructed from the lengths of edges and the angles between the faces of the polyhedron.
If two polyhedra are scissors congruent, then they have to have the same Dehn invariant. So, if Dehn could find two polyhedra with the same volume but different values of this invariant, that would prove the answer to Hilbert’s third problem is no – scissors congruence doesn’t precisely capture 3D volume.

This is exactly what Dehn did, showing that the invariants associated to a cube and tetrahedron with the same volume are different. This means that there’s no possible way to cut up a tetrahedron into a finite number of pieces and reassemble them back into a cube with the same volume.
Are volume and the Dehn invariant all we need to know? If two polyhedra have the same volume and the same Dehn invariant, does that tell us they’re scissors congruent? It took mathematicians another 60 years to answer this question. In 1965, Jean-Pierre Sydler confirmed that the answer is yes, closing this chapter on scissors congruence.
Strange shapes and stranger connections
But the story doesn’t end there. Mathematics is full of shapes living in higher dimensions – like 4D, 100D, 3,485D or any dimension you can imagine – which are impossible to visualize. An active new research area called generalized scissors congruence seeks to uncover whether Hilbert’s question about scissors congruence can also be stated – and maybe even solved – for these strange shapes.

However, what it means for two things to be scissors congruent is now far more complicated. While Hilbert and Dehn cared about things like volume and angles, other mathematicians could exchange these physical traits for something far less tangible.
A recent research program pioneered by mathematicians Jonathan Campbell and Inna Zakharevich proposes a unifying framework for generalized scissors congruence. This framework is built using a very abstract, seemingly unrelated mathematical toolkit called algebraic K-theory.

The big idea of K-theory is that mathematical objects can be understood by how they decompose into fundamental building blocks – much like molecules are broken up into atoms. With a little bit of adjustment, mathematicians can harness the machinery of K-theory and apply it to generalized scissors congruence problems.
This use of K-theory reimagines the problem of scissors congruence and opens the doors for future research. But at the end of the day, scissors congruence is a concrete idea that you don’t need fancy math to understand – just some patience, creativity, a pair of scissors and a lot of tape.

