Albert Einstein made an executive decision to revolutionise our understanding of gravity in a paper published in 1916. Nearly 100 years on, a key prediction of Einstein’s theory has eluded direct detection. A global effort to detect gravitational waves may nostalgically do so on the 100-year anniversary.
Gravitational wave physics holds the key to understanding multiple facets of our universe. Among many other things, gravitational wave experiments have the potential to:
understand the correctness of Einstein’s theory in regions of the universe unable to be observed by other methods
-
directly probe the physics of exotic objects such as black holes, neutron stars, white dwarfs, supernovae, gamma-ray bursts, cosmic strings and so on
provide new and independent tests of cosmology including the rate of expansion of the universe.
The scientific return of gravitational wave science is undeniably massive (although it should be mentioned that the required investment is also high, with individual experiments costing hundreds of millions of dollars).
To understand this scientific potential, we must first understand how gravitational waves are created and detected. For this, we require an understanding of Einstein’s theory of gravity – general relativity.
Einstein’s Relativity
Somewhat counter-intuitively, general relativity asserts that gravity is not a force. Instead, it is the result of objects travelling the shortest possible distance between any two points in a curved geometry. This is not the three-dimensional geometry of space, but that of four-dimensional space-time (i.e. one time plus three space dimensions).
There is a beautiful analogy involving a bowling ball and a marble on a trampoline. Imagine placing the bowling ball on the surface of the trampoline. This acts to curve the trampoline in a region around the ball, analogous to the curvature of space-time around a massive object such as the sun.
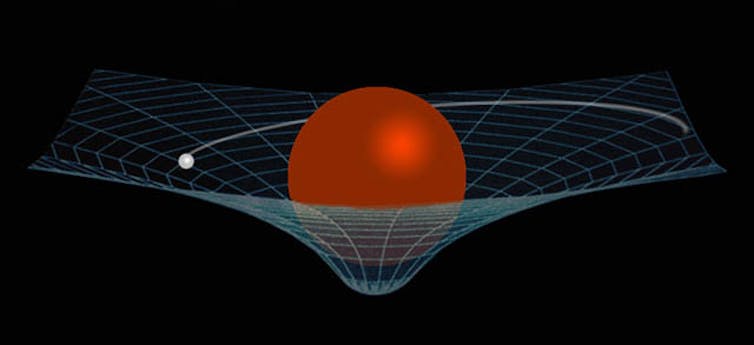
If we ignore friction, we can imagine rolling a marble on the surface of the trampoline such that it orbits the bowling ball. There are no forces acting between the two balls – the bowling ball curves the surface of the trampoline, and the marble simply rolls along geodesics of this curved surface.
Analogously, there are no “forces” acting between the sun and Earth – the sun curves space-time, and Earth travels along a geodesic of this curved space-time.
But what are gravitational waves?
As our small marble rolls over the surface of the trampoline, like ducks swimming through water, very small ripples in the fabric of the trampoline are generated and move away from the marble.
Analogously, when any mass moves through space, ripples are generated in the fabric of space-time that travel away from the moving object at the speed of light. These ripples are gravitational waves.
These waves carry energy from the system, and this fact was used in 1974 to indirectly infer their existence. Russell Hulse and Joseph Taylor measured the orbit of a binary neutron star system with great accuracy, finding that the orbit shrunk by 3mm every eight hours.
This observation matched the predicted energy loss due to gravitational waves with such accuracy that, in 1993, Hulse and Taylor were awarded the Nobel Prize in physics.
How do we directly detect these waves?
Hulse and Taylor’s detection of gravitational waves was indirect, in the sense that they only inferred their existence by ruling out other options. Since the 1960s, physicists have attempted to build gravitational wave detectors that will directly detect their presence.
To understand methods for direct detection, we must first understand the effect a gravitational wave has on particles as it passes.
Consider a ring of particles placed in a perfect circle. A gravitational wave passing will make these particles deform into an ellipse, oscillate back into a circle and then into another ellipse perpendicular to the first. This pattern will continue as the gravitational wave passes through our ring of test particles.

This motion of test masses suggests an obvious method for detection – Michelson interferometry. The nuts and bolts of interferometry involve splitting a single laser beam in two, each travelling at right angles to the other. Each beam travels a certain distance, hits a mirror and returns to the original point at which they split, recombining to form a single beam once more.
If no gravitational wave is present, each beam will travel the same distance, and the combined beam will have a certain interference pattern caused by the recombination of the light. But when a gravitational wave passes through the system, the relative length of each arm will oscillate back and forth, and the resultant interference pattern will display this motion. Sounds easy …
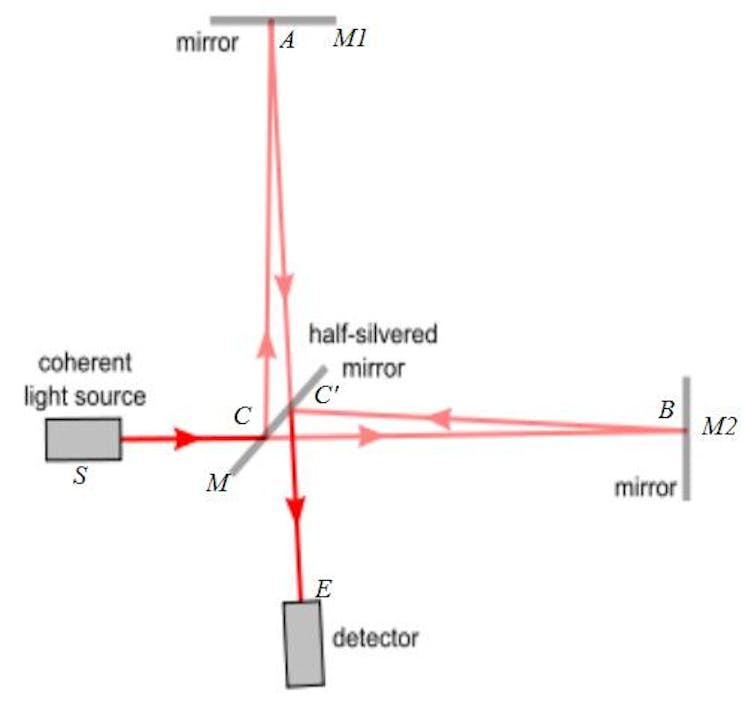
The entire difficulty in detecting gravitational waves is their size.
Our trampoline analogy is again useful. A large bowling ball rolling along the surface of the trampoline will give off significantly larger ripples than our original marble. Likewise, the motion of Earth through space gives off relatively small ripples compared to that of a supermassive black hole.
Exotic events such as supernovae or the merging of two black holes therefore provide the best candidates for the emission of large gravitational waves. And by a “large” gravitational wave, I mean small! The strongest waves change the position of particles by no more than one part in 1,000,000,000,000,000,000,000.
And this is exactly the difficulty in measuring these waves. To successfully detect some of the largest gravitational waves in the universe, we need to measure a change in distance on the order of one part in 1,000,000,000,000,000,000,000. This number explains why it has taken almost 100 years to detect gravitational waves!
A worldwide detection effort
A worldwide network of Michelson interferometers has been built to directly detect these tiny gravitational waves. There is the Laser Interferometer Gravitational-wave Observatory (LIGO), which is a network of three detectors located in the US. There is the Virgo detector located near Pisa, Italy and there is the GEO600 detector near Hannover, Germany.

There are further plans to build gravitational wave detectors in Japan, India and even in space, although these latest plans have been temporarily shelved.
We even have a mini-gravitational wave detector in our own backyard, with active plans to expand to a full-size version in the medium term. The Australian International Gravitational Observatory (AIGO) is a facility for the development of gravitational wave technology located in Gingin, outside Perth.
More than 60 scientists across Australia are active members of the LIGO Scientific Collaboration (a collaboration now totalling more than 800 people) working on topics ranging from laser and mirror technologies to source modelling and data analysis.
(It should also be mentioned that Michelson interferometers are not the only way to directly detect gravitational waves. One of the other most promising methods is through pulsar timing arrays, where the neutron stars are now part of the detector not the source. Australian astrophysicists are leading the world in this field through the Parkes Pulsar Timing Array project.)
Of all the interferometric detectors it is the LIGO/Virgo collaboration that is expected to see first light. These detectors have recently shut down to upgrade to their “advanced” phase, which will give another factor of ten in sensitivity.
The advanced detectors will come online sometime in 2015, giving the very real possibility that gravitational waves will first be directly observed in general relativity’s centenary year.
This is the first of two articles on gravitational waves by Paul Lasky. The second will provide details of the exciting physics, astronomy and cosmology we can learn once gravitational waves have been successfully detected.

