Pourquoi certaines villes atteignent le rang de mégalopoles alors que d’autres stagnent ou disparaissent ? Pourquoi le petit oppidum gaulois de Lutèce est-il devenu la grande métropole qu’est Paris aujourd’hui alors qu’à quelques centaines de kilomètres de là, Autun, fondée par Auguste comme « sœur et émule de Rome » n’a pas dépassé les 20 000 habitants pendant 2000 ans ? C’est une des questions les plus débattues des sciences urbaines.
Une loi historique sur la taille des villes
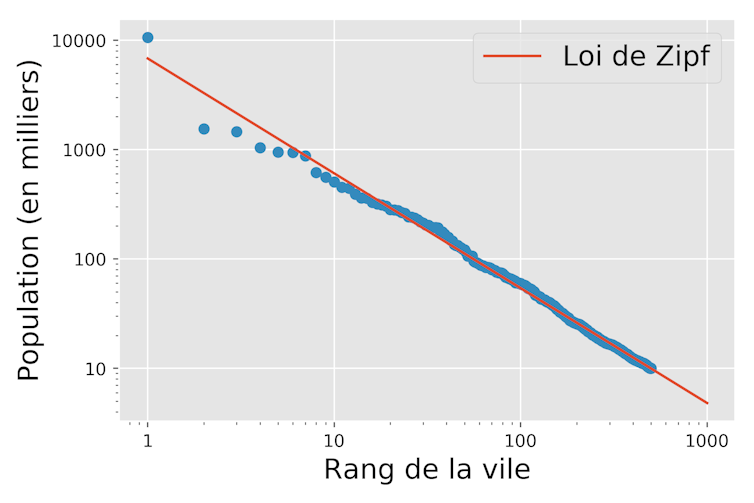
En France, comme dans la plupart des pays du monde, la population urbaine est très inégalement répartie : une ville-monde, quelques grandes villes, un bon nombre de villes moyennes et beaucoup de petites villes. Mathématiquement, la théorie économique décrivait jusqu’ici cette répartition des populations urbaines au sein d’un pays par une loi statistique : la loi de Zipf. Énoncée en 1949 par Georges Zipf, cette loi stipule que si l’on classe les villes d’un pays selon leur population par ordre décroissant (la plus grande ville a donc le rang r=1), la population P d’une ville est inversement proportionnelle à son rang r :
Loi de Zipf (1949) : P=A/r
Ainsi, la ville la plus peuplée d’un pays est-elle généralement deux fois plus grande que la deuxième, trois fois plus grande que la troisième, et ainsi de suite. Cette loi est donc la signature d’une organisation très hiérarchique des villes, avec en général une ville principale beaucoup plus grande que les autres. Cette régularité statistique observée pour de nombreux pays et à de nombreuses époques a déclenché de nombreuses études depuis plus d’un siècle.
Petits chocs quotidiens ou grandes révolutions : qu’est-ce qui marque la taille d’une ville ?
Pour expliquer une telle répartition, une idée naturelle est de faire appel au hasard : les villes d’aujourd’hui sont la résultante d’un très grand nombre d’événements particuliers, qui ont fait prospérer certaines cités et disparaître quelques autres. C’est ainsi que Xavier Gabaix, un économiste français, a proposé à la fin des années 90 une équation qui donne l’évolution de la population en fonction du temps et qui suggère que la loi de Zipf est essentiellement la conséquence naturelle du hasard des naissances et des migrations. Philosophiquement, cela revenait à considérer que les petits chocs du quotidien étaient responsables de l’inégalité des villes, par ailleurs inévitable : certaines villes réussissent et d’autres non. Le problème semblait réglé.
Cependant, la disponibilité et l’ouverture récentes de données démographiques et historiques précises sur les villes a permis de montrer que la loi de Zipf n’était pas toujours vérifiée. Dans beaucoup de pays, en France notamment, on peut montrer que la loi de Zipf est une sorte d’illusion d’optique, une loi qui est facile à voir apparaître quand on se restreint à l’analyse d’un petit nombre de grandes villes. La répartition des populations urbaines est en réalité beaucoup plus complexe et peut varier dans le temps. De plus, les petits chocs du quotidien de Gabaix ne suffisent pas à expliquer les grands chocs urbains historiques : ruée vers l’or, épidémies majeures, villes-nouvelles, déshérence industrielle. Si la répartition des villes est bien le résultat du hasard, encore faut-il savoir de quel hasard on parle : celui qui s’accumule tous les jours ou celui qui en très peu de temps bouleverse le paysage urbain.
En analysant les données démographiques et de migrations pour plusieurs pays et sur plusieurs périodes (France 2003-2008 ; 2012-2017 USA ; 2012-2016 Royaume-Uni ; 2012-2016 Canada), nous avons pu quantifier les différentes contributions à l’évolution de la population urbaine : le bilan démographique (naissances et décès), les migrations internationales, et les migrations interurbaines (les déménagements d’une ville à une autre dans le même pays). À partir de ces résultats, nous avons écrit une nouvelle équation qui décrit l’évolution temporelle des populations urbaines d’un pays.
Des grands chocs décident du destin des villes
Nous avons alors montré que ce sont les grands chocs migratoires interurbains qui gouvernent les variations temporelles des populations urbaines. Ces chocs sont rares mais suffisamment importants pour changer le destin des villes, les faire émerger ou disparaître. Par exemple, pendant la ruée vers l’or, la population de San Francisco passe d’un peu plus de 1000 à 150 000 habitants entre 1850 et 1870. Plus près de chez nous, la population du Creusot (d’ailleurs pas très loin d’Autun) est plus que décuplée entre 1831 et 1856 par l’implantation de la famille Schneider.
Nos travaux, publiés récemment dans la revue Nature permettent d’apporter un regard nouveau sur le destin des villes. Ce ne sont pas les petits mais les grands événements qui font la démographie urbaine et qui décident du sort des villes d’un pays. En particulier, ce sont les vagues de migrations urbaines, ponctuelles mais majeures, qui expliquent pourquoi certaines villes émergent et d’autres disparaissent.
Finalement, cette équation porte un message optimiste : elle montre que le destin d’une ville n’est pas figé et ne dépend pas uniquement de sa démographie. La réussite des villes s’explique davantage par des chocs extérieurs, éventuellement induits, et maîtrisables, que par l’accumulation d’effets strictement aléatoires et fatals. Les décisions de politique et de planification urbaine ont donc un rôle majeur à jouer pour renforcer l’attractivité d’une ville et peuvent complètement modifier sa dynamique d’évolution et son histoire future.
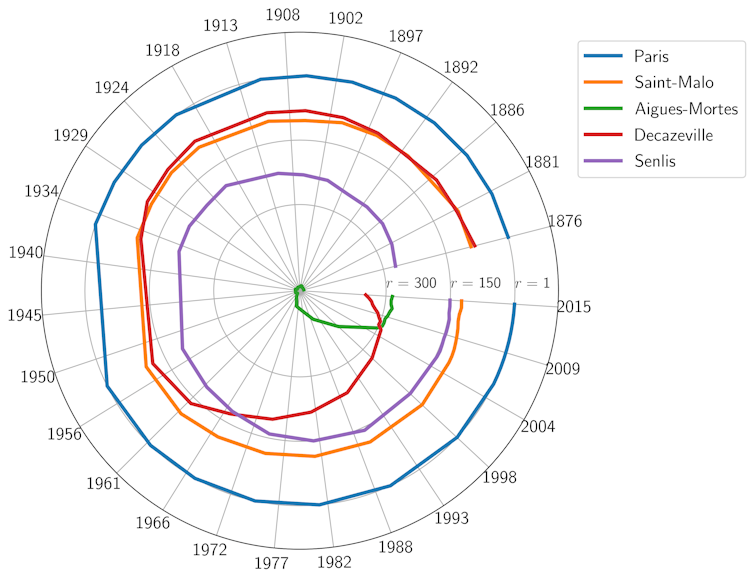
Horloge des rangs
Pour visualiser l’évolution de la population d’une ville au cours du temps, on peut représenter le rang r d’une ville (le « classement » de la ville par population) sous la forme d’une horloge. Pour chaque année, le cadran fait figurer le rang de la ville correspondant. Une ville qui ne change pas de rang est donc représentée par un cercle tandis que le rang d’une ville qui croît ou décroît relativement plus vite que les autres prend la forme d’une spirale. Plus la spirale est resserrée, plus le changement s’opère brutalement. Nos travaux prédisent que ces spirales resserrées arrivent beaucoup plus souvent qu’on ne le pensait jusqu’alors.