While some first political and economic consequences of the Brexit vote are already visible, London’s role in the world financial markets has been so far relatively unaffected. The high density of financial institutions combined with a longstanding tradition of the banking industry makes the role of the City in the financial arena rather stable.
Among the several indexes located in this financial powerhouse is the ICE London Interbank Offered Rates – commonly known by its acronym, LIBOR. Since the 2008 rigging scandal there has been some discussion of phasing it out, but it remains a key index in the world’s financial markets.
Each LIBOR rate determines the interest rate at which banks lend each other money for some length of time (ranging from 1 day to 12 months) on different currencies (dollars, euros, etc.). These benchmark rates are widely used as a base interest rates by financial institutions all over the world since many contracts are paid at least the interest corresponding to some LIBOR rate.
Therefore, the LIBOR rates impact directly and indirectly small businesses as well as corporations, the world’s largest banks and almost any financial product such as loans, mortgages and derivatives. Arguably, the LIBOR rates are among the world’s most important numbers. It is often thought as a good barometer of the global economic and financial situation.
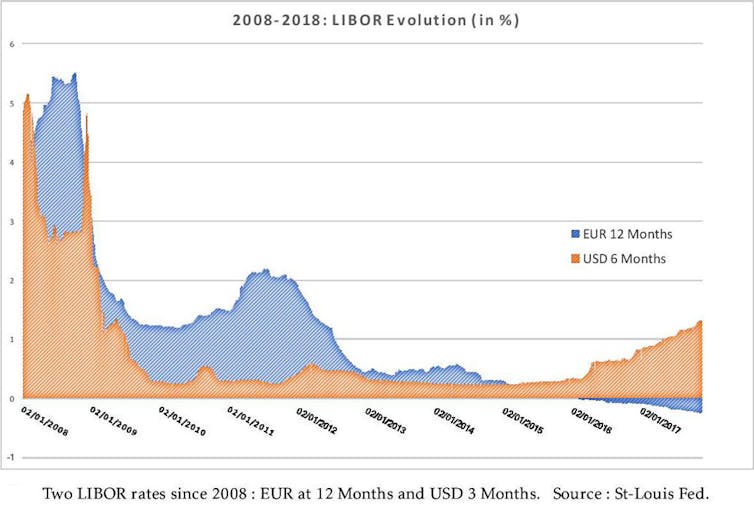
Figure 1 depicts the evolution of two of these rates since 2008: the one corresponding to loans in euros for 12 months and the one corresponding to loans in US dollars for three months. One can distinguish clearly three different regions. In first one, spanning from the beginning of 2008 until mid 2010, where both indexes are in decline, corresponds to the aftermath of the subprime financial crisis. The second period, that ends at the beginning of the year 2015, corresponds to some stable period in which both rates do not move much the EUR12 being higher than the USD3 one. The final region, that lasts until today, corresponds to an unusual period in which the EUR12 is negative while the USD3 is positive and increasing. What can one infer from these indexes ? How is each index determined?
Elections and manipulations
A distinct feature of these rates is that its value is not determined through a market but through an election. More precisely, a daily election is held in which a selected sample of 18 banks takes part. Each bank reports a value (interest rate) which represents the rate at which it is ready to lend money in this currency for certain amount of time. The extreme reports (the top and the bottom four) are removed and the LIBOR corresponds to the average of the remaining values. Figure 2 explains this computation with five banks and the deletion of the top and the bottom value.

The logic of the LIBOR computation is made transparent in Figure 2: the first step, dropping the extreme reports, invalidates the extreme reports whereas the second one simply averages the moderate ones, leading to a LIBOR of 0.527%. The role of the second step is to represent in a consensual manner the moderate values. In a sense, one could argue that this method tries to give incentives for consensus since none of the banks has an interest in announcing a value too different from the rest of the announcements. Yet, since the financial crisis in 2008, manipulation in the LIBOR (often referred to as the LIBOR scandal) casts some doubts over the way this index is determined.
In the 2008 LIBOR scandal, some banks altered their reports so as to obtain a value that fitted better their own interests. For instance, a report by the United Kingdom Financial Services Authority (FSA) stated that:
“Barclays’ misconduct was serious, widespread and extended over a number of years. The integrity of benchmark reference rates such as LIBOR and EURIBOR is of fundamental importance to both UK and international financial markets. Firms making submissions must not use those submissions as tools to promote their own interests”.
If every bank announces honestly its preferred interest rate, this method is arguably close to perfect. However, a reasonable question is whether banks have the incentives to do so under this method. If not, this casts some shadow over this manner of computing LIBOR.
To understand the logic of a manipulation in a simple manner, consider that in Figure 2 every bank is honestly announcing its preferred interest rate. For instance, this implies that Société Generale’s preferred rate is 0.52%. What is the consequence of a misreport with this system? As long as the report is not too extreme, that is located in between the ones of Rabobank and Crédit Suisse, a misreport (or strategic report) affects the outcome. If for instance, S.G. announces 0.499, then the final outcome is 0.52: namely, by misreporting, S.G. obtains its preferred rate (see Figure 3 for an explanation). This leads to the following conclusion: the classical method for computing LIBOR gives banks incentives not to report their preferred interest rate but rather to strategise as a function of the expected reports of the rest of the banks.

A proposal
Can we find reasonable ways of building the LIBOR rate without this undesirable feature? One can always design sophisticated methods to check whether the reported values are indeed sincere, yet this comes at the cost of thin auditing methods which can be rather inefficient. Yet, this method will still lie in the setting in which banks are always tempted to manipulate the true valuation, which might in turn create new problems with fake reports. Our view is that the purpose of the LIBOR method is to design a method which is simple and practical while at the same time it represents well the different preferences of the banks. Namely, if one wants to improve the computation of the LIBOR, one needs to design an instrument that moderates the final decision while it leads to a consensual final rate.
This has led us to design methods that escape from the dilemma of reporting the true value versus manipulating via reporting a strategic value. One of these methods works as follows: each bank reports a range of values and not anymore, as in the original LIBOR, a single value. Namely, rather than reporting 0.52 and 0.499 as in Figures 2 and Figure 3, the Société Générale is now allowed to announce any range of interest rates: for example, in Figure 4, S.G. announces any value from 0.231 until 0.841. This means that S.G. approves of any value in this interval.
The interval method computes the LIBOR in a different manner. Rather than dropping values, it considers the different intervals announced by the different banks as a sample of points (see Figure 4b). Given this sample of points, it plots the distribution of the approvals made by the different banks (Figure 4c). Finally, it selects the value that divides in two exact halves the sample of points generated by the banks’ announcements.
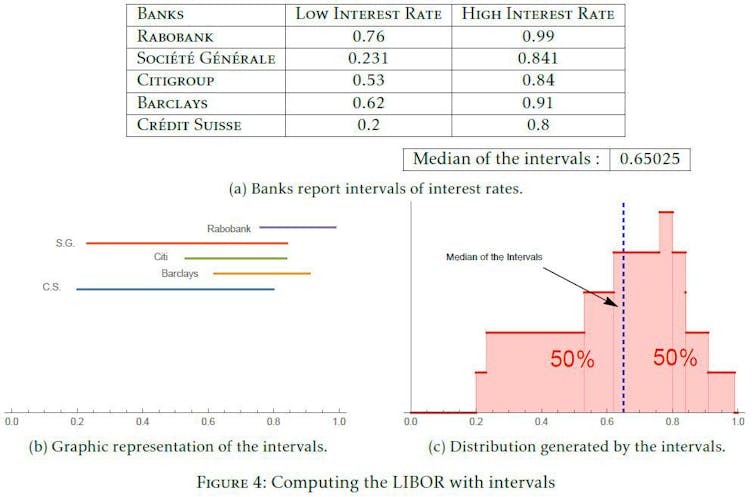
How should we expect banks to behave under this method? Theoretically, this method should lead to selecting (a very accurate estimation of) the median preferred interest rate of the banks. The idea behind the median interest rate is quite familiar in economics and political science: the Condorcet winner. Consider the ideal point of each bank and order them from the lowest to the highest one. The median interest rate is the one that divides the sample of ideal points in two exact halves since half of these values are lower than the median interest rate and half are higher. An important property of the median interest rate is its democratic appeal: it turns out that if one starts comparing by pairs each of the ideal points of the different banks, the only interest rate that defeats by a majority any other ideal point is the median interest rate. It is hence a basic desideratum for respecting the will of the banks to ensure that the outcome is as close as possible to the median of the ideal points.
This convergence to the median should occur since a bank’s ideal strategy is to announce either all the interest rates to the left of the outcome or all the alternatives to the right of it. The bank should theoretically announce all alternatives located to the left of the outcome if its interest rate is lower than the outcome whereas it announces all alternatives to the right of the outcome if its ideal interest rate is higher. In practice, few are known.
Some experiments have been run in the Cyprus Experimental Economics Lab at the University of Cyprus, and while it is still early, the first available results are encouraging. In a lab setting, we endow players with a minute to decide over the interval they want to announce. During this period of time, they are allowed to play with the intervals while seeing in real-time the announcements of the rest of the players. Most experimental subjects tend to understand well the mechanism and the outcome is quite close to the median of the players’ ideal points. More importantly, players seem to be much more satisfied with the final outcome than with the usual methods so that the method increases the consensual views of the different players.
Final remarks
The LIBOR rates are core tools in the global financial system. It is then essential to ensure that these rates are well-calibrated so that they reflect well the will of the different banks involved in its construction. While the LIBOR scandal underlined some weaknesses in the initial method of computation, a myriad of possible fixes might be available. Our proposal is to offer each of the banks more flexibility, allow each to announce ranges of interest rates. While more evidence is needed on the benefits of this system, the current theoretical and experimental results make this approach a potentially interesting one. A key advantage is that banks would no longer face the usual dilemma between being sincere or opting for their self-interest, removing any potential auditing costs.

