Christmas 1840, cold and crisp. The fashionable and wealthy Lovelace family are learning to skate, the four year-old Byron (junior, the grandson of Lord Byron) pushing a chair along the ice to keep his balance. Driven inside by the cold, his mother retires to her study and her lessons in advanced calculus. She writes to her tutor: “This is very mathematical weather. When one cannot exercise one’s muscles out of doors, one is peculiarly inclined to exercise one’s brains in-doors.” Then she plunges into a detailed discussion of the convergence of series.
Her name is Ada, Countess of Lovelace. Her teacher was Augustus De Morgan, one of the foremost mathematicians of the day. She is studying the material he taught his advanced class at the then all-male University College London: he writes of her power of thinking as “utterly out of the common way”, capable of grasping the “real difficulties of first principles”.
This grounding in advanced mathematics was essential for Ada Lovelace’s most famous work, a paper published in 1843, which translated and considerably extended a work by please by Luigi Menabrea about a general-purpose mechanical computer designed by Charles Babbage, his unbuilt analytical engine. The substantial appendices written by Ada Lovelace contain an account of the principles of the machine and a table often described as “the first computer programme”. Lovelace presents the machine, not in terms of ironmongery, but as what we would now call an “abstract machine”, describing the functions of memory, CPU, registers, loops and so on.
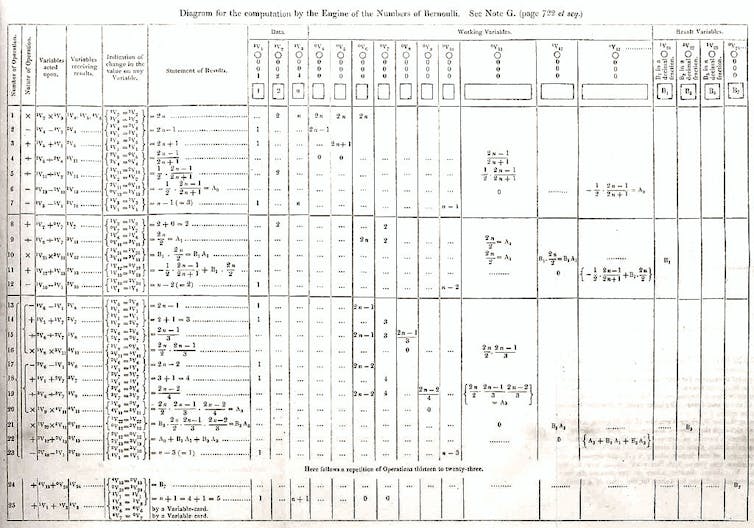
What is truly remarkable to the modern computer scientist is her high-level view. She understands the complexity of programming, the difficulty of checking correctness and the need for programme optimisation. She reflects on the power of abstraction, how the machine might “weave algebraical patterns”, how it might work with quantities other than number and its potential for creativity. In what Turing later described as “Lady Lovelace’s objection” to whether machines can think, she observed that: “The Analytical Engine has no pretensions whatever to originate anything. It can do whatever we know how to order it to perform.”
Ada, Countess of Lovelace, was born Ada Byron on 10 December 1815, the daughter of the poet Lord Byron and his wife Annabella (nee Milbanke), and died after a long and painful illness in 1852. In 1833 she married William King, who was created Earl of Lovelace in 1838. Although her parents separated when she was a few months old and she never knew her famous father, his notoriety as “mad, bad and dangerous to know” has often overshadowed accounts of her life.
From an early age, Lovelace showed a passion and a talent for mathematics and science. Her mother was a noted educational reformer and organised her own daughter’s education on the principles of Pestalozzi. This involved the study of mathematics, French and music accompanied by childhood visits to factories and workshops. This later helped Lovelace grasp the mechanical principles of Babbage’s calculating machines, which she first encountered in her teens.
In later life, Lovelace continued to pursue her mathematical interests. She contributed to her husband’s writings on crops and husbandry, proposing a quadratic, rather than a linear, model to relate growth of plants to quantity of sunlight. She followed the latest scientific trends, like photography and mesmerism, and even suggested that collecting amateur photographs of mesmeric phenomena would aid scientific understanding – an early example of crowdsourcing. She wanted to understand the workings of the mind and wrote about whether there might be mathematical laws underlying the operations of the brain, a “calculus of the nervous system”.
Lovelace’s name lives on through the Ada programming language as well as initiatives for women in science, including the annual “Ada Lovelace Day” in mid-October. She has become a controversial figure, generating both wild enthusiasm and, in turn, a backlash of hostility, to extravagant claims that she foresaw quantum mechanics, invented the CD, or brought about Silicon Valley.
But there is no need to exaggerate – in her 200th year we should celebrate an extraordinary individual, who defied the constraints of her time and gave a remarkable and farseeing account of the principles, potential and challenges of computation.
We know so much about Ada Lovelace and her world because of a large archive of family papers held at Oxford’s Bodleian Library. The wonderful insights they offer into her relations with her family and children, her variety of interests and her sometimes intense feelings, have perhaps obscured their contribution to the history of science and mathematics. But Lovelace offers much further potential for true collaboration between the humanities and the sciences to understand the scientific and cultural context for the emergence of modern ideas of computation.

