There is likely no topic in Canada at the moment that is more acrimonious than elementary school mathematics education. The entire country, it seems, is divided.
On one side, there are those who are enraged by the so-called “new math” that has been held simultaneously responsible for a) diminished achievement by students and b) frustration among parents who feel helpless in the face of unfamiliar strategies.
On the other side are those who insist that math must make sense to today’s students — children who have grown up in a digital age, are adept with multiple technologies and will likely never be required to perform long division.
As a researcher who is deeply committed to engaging parents as partners in mathematics education, I spend many evenings on the road. I work with school staff and school councils across the province of Ontario to support parents in their efforts to help their children learn and love mathematics.
In communities from Chesterville to Picton, Guelph to Thunder Bay and Courtice to Fort Frances, I have encountered the same question repeatedly: What are you teaching my child?
Arithmetic from Mexico to Japan
The question is always sincere. The rationale differs considerably, but in most cases, the question arises because the computational strategies that the child is using to perform multi-digit calculations look very different from those learned by the parents, resulting in confusion and mistrust.
Experience has taught me to give a quick mini-lesson on arithmetic around the world to emphasize that there is no one global set of rules for calculations.
For example, I show a method that was used in Mexico, called “llevamos uno” — we carry one. Instead of noting ones or 10s to be “carried” at the top of the next column, students were taught to note those figures to the right side of the problem.
1 9 4
+ 3 9¹¹
2 3 3
I share a method that I learned from the Philippines, where students use dashes to indicate groups of 10.

Finally, I share a Japanese “scratch method” that is similar to the one used in the Philippines, but instead of dashes, overstrikes are used to keep track of groups of 10s. In addition, the leftover amounts are indicated by the use of subscripts.
2 6
7₁ 6₂
+2 8₀
1 3 0
Again, we begin at the right, at the top of the column: six plus six is 12, which is 10 (strike through the six) and two is left over (subscript two); two plus eight is 10, (strike through the eight) and zero (subscript zero). Write the zero under the ones column, and carry two groups of 10; two (10s) and two is four, plus seven (10s) is 11. Strike through the seven (to represent 100) and record one (subscript one). One plus two is three. Write the three in the 10s column and carry one group of 100. The answer is 130.
We read left to right
Having made the point that there is no universal set of rules to add multi-digit numbers and that all unfamiliar methods (including those used by their children) seem complex and incomprehensible at first glance, I am able to emphasize two important reasons to support new strategies for multi-digit addition.
When I ask parents to reflect on how they read to and with their toddlers, the answer is immediate and consistent: From left to right, using their index finger to trace the direction of the words.
Then I ask them what happens when we introduce children to the task of adding two-digit numbers. The light bulbs go on. We teach them to work right to left.
“Why?” I ask.
Dead silence or: “Because.”
In our number system, the value of a digit depends on its place, or position, in the number. So, for example, the number 4,276 is made up of 4,000 + 200 + 70 + six. Children who understand place value, i.e., that the value of a digit (zero to nine) depends on its position in a number, can easily decompose a number — an important strategy for mental math.
It’s ironic that after months of teaching the importance of place value, a fundamental concept in math, we do not apply that knowledge in practical ways to simplify multi-digit addition. As soon as we introduce questions like …
8 7
+ 6 5
… we instruct students to begin at the right. This is in conflict with everything that children have been taught about reading from left to right and the importance of place value, i.e., that we read numbers from left to right, in order of magnitude. The algorithm, in fact, leads children to “unlearn” everything they know about place value.
Building on children’s understandings
Multi-digit arithmetic makes sense when we add from left to right, applying what we know about place value and reading.
6 7
+ 2 4
8 0
1 1
9 1
In this case, we add the 10s column first, 60 plus 20 to get 80. Next, we add seven to four to get 11. Add 80 and 11 to get the sum. This eliminates the need for “carrying” because the numbers align according to their value.
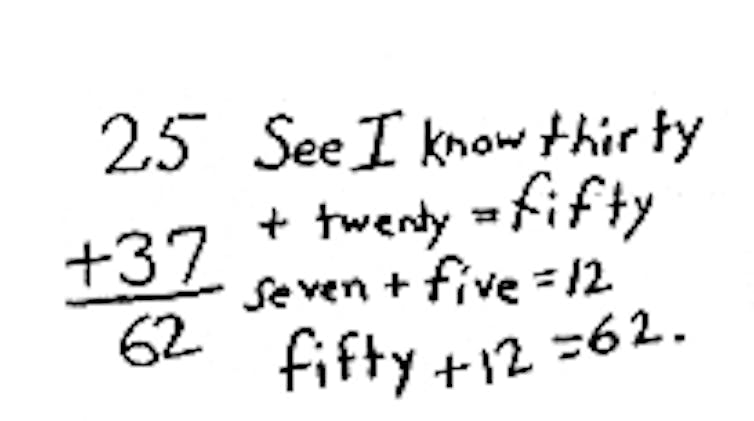
Children respond positively to this strategy because it makes sense. It builds on their understanding of place value and how numbers are made.
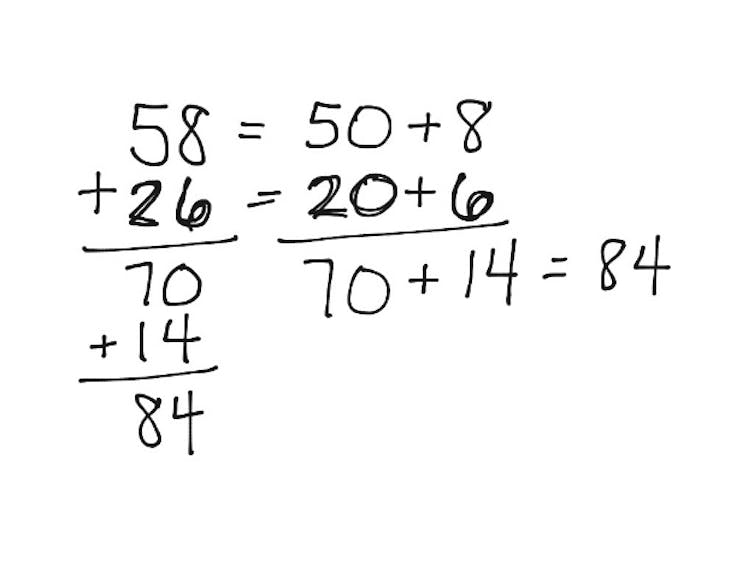
Why are parents so resistant to such strategies? The traditional algorithms are used by adults in their peer group and come from adults whom they respect. This may attach an aura to the traditional methods as the “real” or ultimately correct way to compute.
As mathematics education giant John van de Walle once noted, it’s difficult to ignore the power of adding “the way my dad taught me.”
But it’s time to ask: Are the traditional algorithms really necessary? Or are we holding our children back by our own fears and lack of understanding of the alternatives?

