Some of my earliest football memories come from the 1994 World Cup, when my dad helped four-year-old me complete the tournament sticker album. Romario, Gheorghe Hagi and Roberto Baggio were the stars, but names like Marco Etcheverry, John Harkes and Marco Pascolo are every bit as memorable to me – since they helped me complete that book.
Now, almost 30 years later, many children around the world will be collecting stickers during the Euro 2020 tournament.
Sticker albums are a curious yet enduring part of football fandom, often holding nostalgic value for supporters like me. When a major football tournament rolls around, fans buy books with spaces for stickers of the players. The aim is to fill every space. But stickers are sold in packs of six, all randomly chosen.
Fans can easily end up with ten copies of one sticker while others remain difficult to track down. Fans start to associate the tournament as much with these tricky stickers as the top goal scorers.
I like to think sticker collecting played a small part in leading me to become a statistician. It is, after all, based on statistical probability.
The Euro 2020 album has a whopping 678 stickers to collect – including pictures of the players from all 24 competing nations plus photos of the trophy and official mascot. Each collector hopes to reach the full set, and it isn’t as simple as just buying the ones you need.
Statistics can help us work out the cost of finding every sticker. To get 678 you’d need to buy 113 90p packets, which comes in at £101.70. But the chances of having no duplicates is so slim it can basically be considered impossible.

Read more: European Super League failure was a lucky swerve for women’s football
It’s guaranteed our first sticker will be a new one, making the probability of success 1. For our second sticker the probability is 677/678, since there are 678 possible stickers and 677 would be new.
To calculate the probability of completing the album without duplicates, we multiply (678/678) by (677/678) by (676/678), and so on until (1/678). This gives us a 1 in 4.33 x 10²⁹² chance (4.33 followed by 292 zeroes), which is an unimaginably tiny number.
Now we know 113 packets isn’t going to be enough, how many packets do we need to buy? There’s no exact answer, but statistics can help us work out the probability of completing the album if we buy a certain number of packets.
The likely cost
We want to answer the question: “if we take a given size of sample of stickers from a set of 678 possible stickers, what is the probability of finding each of the 678 stickers at least once?”.
A formula exists to compute this probability, but it’s not simple. It contains something called the factorial of 678 – which is 678 multiplied by 677 by 676, and so on until one. Unfortunately, this number is so large even a powerful computer can’t calculate it. This is very common in statistics, and there are techniques for estimating probability when this happens.
One approach is a simulation, using a computer to repeatedly recreate the sticker collection process by virtually opening packets and working out whether we reach all 678 stickers. If we repeat this process often enough – I did it 100,000 times in this example – we’ll get a very good estimate of the true probability.
The outcome of my simulation makes for eye-watering reading for sticker collectors.
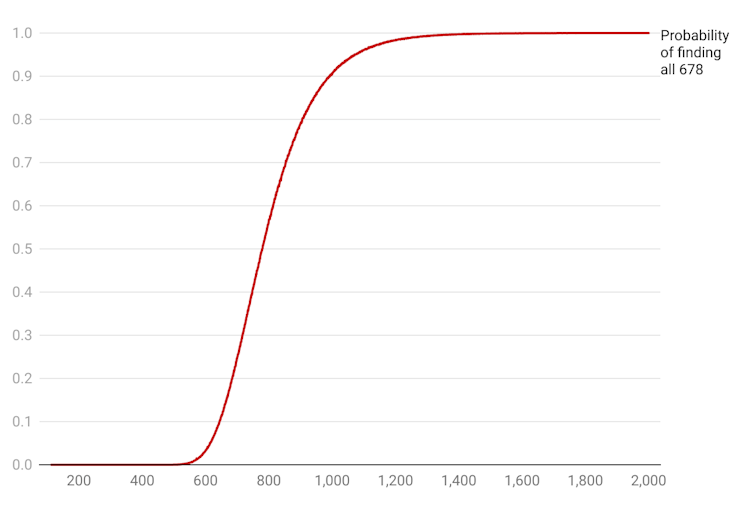
If you want a 50% chance of completing the album you need to spend £702 on 780 packets of stickers. To raise your probability to 75%, it’ll cost you £790.20 (for 878 packets) and a 90% chance of success will set you back £893.70 (for 993 packets). The probability of success will never be 100%, but you’d be exceptionally unlucky not to find them all if you bought around 2,000 packets.
My simulation showed the median number of packets you had to buy to complete the album was 778, at a cost of £700.20. The cheapest cost across 100,000 simulations was £406.80 (452 packets) while the most expensive was £1,961.10 (2,179 packets).
Make it cheaper
Getting the final few stickers is the most costly part. If you still have 51 left, the odds of finding one of them is 51 out of 678 (or 7.5%), whereas if you have one left to find the chances are 0.15% (one out of 678).
Collectors can buy up to 50 named stickers, for 28p each. This means you only have to find 628 stickers to complete your album.
With this in mind, you only have to buy 295 packets (at a cost of £265.50) for a 50% chance of completing the album, 304 packets (£273.60) for a 75% chance and 313 packets (£281.70) for a 90% chance. Once you’ve bought around 350 packets you’d be extremely unlikely not to complete the album. Even adding on the £14 to buy the remaining 50 stickers, you can make an enormous saving.

Another way you can reduce the cost is swapping stickers. Trading costs nothing – you’re giving away a duplicate you’ve already paid for. If you’re very shrewd about how you trade, you shouldn’t need to buy more than the 113 packets.
Sticker collecting can be a very expensive habit, setting you back over £100 for a tournament – and more if you don’t have anyone to swap with. But, it can introduce children (and adults) to the concept of probability.
From my own experience it can also be a great way to build an emotional connection with a wonderful sport. You can’t put a price on education or the chance to create shared memories and a lifelong obsession with football. As soon as she is old enough, I will be collecting stickers with my daughter.

