Recently, I was asked by a parent how old children should be to learn how to multiply numbers. He was shocked when I said that children in kindergarten may be experts in multiplication.
It’s not uncommon for young children to recite preliminary “times tables” as they “skip count” aloud. “Two, four, six, eight, 10” and “three, six, nine, 12” are among the first steps in learning about multiples.
In fact, adults can support skip counting by using two tools found in every home: A calculator and a clock.
Your child can “teach” the calculator to skip count by four, for example, simply by entering “4” on the calculator, next pressing “+” and “4” and then pressing the equal sign repeatedly.
You can follow along as the display changes from four to eight to 12 to 16 to 20, representing the multiples of four in the four times table. To count by six (or any other number), just change the starting number and the first addition number.
Alternately, you and your child can discover the five times table on the face of an analog clock. It’s easy because the clock has five minute increments and is numbered from one to 12. The number of minutes correspond to the multiplication fact, so, for example, 5 X 5 = 25. This also helps children learn to read time.
Creating muscle memory in the brain
These “kitchen table” family math activities are examples of strategies that offer repeated practice while making the task of learning the times tables more fun and engaging.

More importantly, these and other “Let’s Play Math” fact games serve to create “muscle memory” in the brain, simultaneously making it possible for students to retain their number facts and laying the groundwork for more complicated computations and applications down the road.
Familiarity and proficiency with the basic times tables are an essential building block in math.
It opens the door to multi-digit multiplication and demystifies processes like long division and simplifying fractions. It lays the foundation for algebra.
‘Math makes sense’ approach
At workshops, I often ask teachers and parents to look at the following examples of student work from education scholar Deborah Ball. I ask them to identify which of these students would they judge to be using a method that could be used to multiply ANY two numbers and explain why.

In the first case, Student A multiplies from the top down, from right to left:
5 X 25 = 125 and 3(0) X 25 = 75(0).
Fortunately, the student gets the right answer, largely due in part to the simple multiplications (students relate multiplying 25 to using 25 cent coins) and because she positioned the 75 correctly.
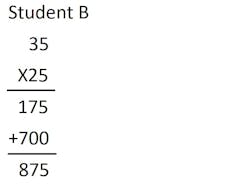
Student B multiplies from right to left:
5 X 35 (mentally calculating 2 X 35 = 70, so 4 X 35 = 140, so 5 X 35 = 140 + 35 or 175) and 20 X 35 (getting 700) then adds the partial sums together to get the final product.
The strategy produces a “right answer” but the student’s “work” is not transparent.
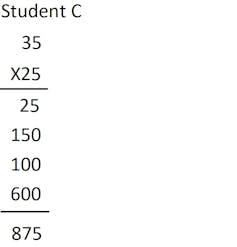
Student C uses a step-by-step place value process that will ALWAYS work:
The student multiplies 5 X 5, then 5 X 30, then 20 X 5 and 20 X 30 to get 25 + 150 + 100 + 600 which sums to 875.
This “math makes sense” approach to multi-digit multiplication (also called the “partial products method”) appeals to students because it values their prior learning by putting their basic number facts to use, logically and efficiently.
It does not require any unnecessary “carry the one and move to the left, adding zeroes as place holders” line-by-line rules, and it is universal.
It works for numbers of any magnitude because of its mathematical simplicity, elegance and, most importantly, generalizability.
Eyes on the future
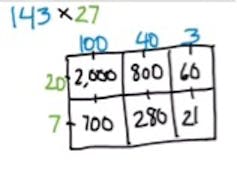
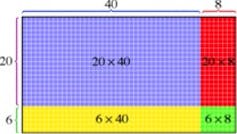
The mathematicians and education researchers who have helped classroom teachers to implement this straightforward computational procedure are eager to emphasize that their enthusiasm is due, in part, to their “eyes on the future” — focused on secondary and post-secondary mathematics.
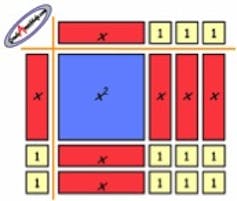
The “place value” model for multi-digit multiplication (which works left to right or right to left) can be represented visually using the “area” model of multiplication.
As students move through the grades, the “area” model of multiplication becomes increasingly important.
The transition from …
Table [(100 + 40 + 3) X (20 + 7)] to
Grid [(40 + 8) X (20 + 6)] to
Algebra [(x + 3) X (x + 2)]
… follows a natural progression with respect to mathematical sophistication.
Breaking the math barrier
Recently, we have seen many “pro” mathematics movements across the continent and the globe: For example, With Math I Can and The Global Math Project.
In these, we have seen a renewed emphasis for efforts to support ALL children to be successful mathematics learners, and, by so doing, break down the math barrier that has been shown to limit success in school, career and life.
For that to be possible, all children must learn their times tables.
Being able to recall basic facts efficiently is a necessary first step in the development of more advanced skills for computational fluency with larger numbers and algebraic expressions.
Diagrams, charts, procedural models and representations using concrete materials like algebra tiles (which are the visual and concrete descriptions of the multiplication of multidigit numbers and algebraic terms) are only possible when place value applications as well as number properties and patterns can be put into operation (figuratively and literally) by students.
And that requires students to understand connections by appreciating the meaning, significance and application of even the simplest number fact in computing a correct calculation.
And that means that elementary school multiplication is anything but elementary.

